Fiducial distribution
A distribution  of the parameter
of the parameter  from a family of distributions
from a family of distributions  of an observation
of an observation  . It was introduced by R.A. Fisher [1] for numerical
. It was introduced by R.A. Fisher [1] for numerical  and
and  in the case when the distribution function
in the case when the distribution function  of
of  decreases as
decreases as  increases in such a way that
increases in such a way that 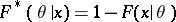 , considered as a function of
, considered as a function of 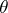 for fixed
for fixed  , has the properties of a distribution function (in such a situation one often makes use of a sufficient statistic in the role of
, has the properties of a distribution function (in such a situation one often makes use of a sufficient statistic in the role of  ).
).
A fiducial distribution is defined for invariant families of distributions (cf. [2]–[4]). Namely, suppose that a group 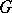 of transformations
of transformations  acts on the sets
acts on the sets  and
and  . A family of distributions is called invariant if
. A family of distributions is called invariant if  has the distribution
has the distribution  when
when  has the distribution
has the distribution 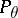 . In this case one considers equivariant decision rules
. In this case one considers equivariant decision rules  (i.e. such that
(i.e. such that  for all
for all  and
and  ) and invariant loss functions
) and invariant loss functions  (i.e. such that
(i.e. such that 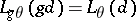 for all
for all  ,
,  and
and  ). If the action of
). If the action of  on
on 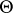 is transitive, then the family
is transitive, then the family  has a certain property of homogeneity: For a fixed parameter value
has a certain property of homogeneity: For a fixed parameter value 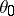 and an observation
and an observation  with the distribution
with the distribution  , the distribution of
, the distribution of 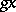 runs through the whole family
runs through the whole family  as
as  runs through
runs through  . Suppose that
. Suppose that 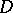 is a set of probability measures on
is a set of probability measures on 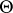 (it is assumed that
(it is assumed that  -algebras
-algebras  and
and  are given such that the transformations in
are given such that the transformations in 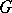 are measurable). Let the action of
are measurable). Let the action of 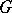 on
on  be given by
be given by 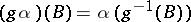 ,
,  . The fiducial distribution is described by the family
. The fiducial distribution is described by the family 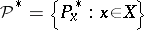 of probability measures on
of probability measures on  that minimize the risk
that minimize the risk 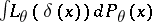 in the class of equivariant decision rules for every invariant loss function satisfying the following condition of unbiasedness type
in the class of equivariant decision rules for every invariant loss function satisfying the following condition of unbiasedness type
 |
If  acts transitively on
acts transitively on  , then the family of the fiducial distributions is uniquely distinguished by the requirements that
, then the family of the fiducial distributions is uniquely distinguished by the requirements that  is invariant and that the probable and fiducial probabilities are equal,
is invariant and that the probable and fiducial probabilities are equal,  , for invariant families
, for invariant families 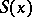 (
(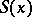 is called invariant if
is called invariant if 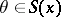 ,
, 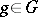 imply that
imply that  ).
).
References
| [1] | R.A. Fisher, "Inverse probability" Proc. Cambridge Philos. Soc. , 26 (1930) pp. 528–535 |
| [2] | D.A.S. Fraser, "The fiducial method and invariance" Biometrika , 48 (1961) pp. 261–280 |
| [3] | G.P. Klimov, "On the fiducial approach in statistics" Soviet Math. Dokl. , 11 : 2 (1970) pp. 442–444 Dokl. Akad. Nauk SSSR , 191 : 4 (1970) pp. 763–765 |
| [4] | G.P. Klimov, "Invariant inferences in statistics" , Moscow (1973) (In Russian) |
Comments
There has been a continued controversy as to what Fisher really meant by fiducial distributions, many authors finding the idea quite meaningless. See, e.g., [a1] for a recent survey.
References
| [a1] | J.G. Pedersen, "Fiducial inference" Internat. Stat. Rev. , 46 (1978) pp. 147–170 |
Fiducial distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fiducial_distribution&oldid=18272