Fibre space

An object , where is a continuous surjective mapping of a space onto a space (a fibration). , and are also called the total space, the base and the projection of the fibre space, respectively, and is called the fibre above . A fibre space can be regarded as the union of the fibres , parametrized by the base and glued by the topology of 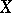. 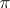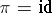For example, there is the product , where is the projection onto the first factor; the fibration-base , where and 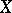is identified with 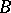; and the fibre space over a point, where is identified with a (unique) space .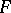

A section of a fibration (fibre space) is a continuous mapping such that .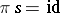

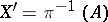The restriction of a fibration (fibre space) to a subset is the fibration , where and 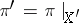. A generalization of the operation of restriction is the construction of an induced fibre bundle.

A mapping is called a morphism of a fibre space into a fibre space if it maps fibres into fibres, that is, if for each point there exists a point such that . Such an 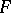determines a mapping 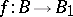, given by . is a covering of , and ; the restrictions are mappings of fibres. If and 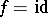, then is called a -morphism. Fibre spaces and their morphisms form a category containing the fibre spaces over and their -morphisms as a subcategory.

Any section of a fibration is a fibre space -morphism from 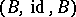into . If 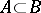, then the canonical imbedding is a fibre space morphism from to .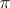

When is a homeomorphism, it is called a fibre space isomorphism, a fibre space isomorphic to a product is called a trivial fibre space, and an isomorphism is called a trivialization of .

If each fibre 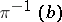is homeomorphic to a space , then is called a fibration with fibre 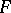. For example, in any locally trivial fibre space over a connected base , all the fibres are homeomorphic, and one can take to be any ; this determines homeomorphisms .

Comments

Both the notations and 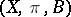are used to denote a fibration, a fibre space or a fibre bundle.

In the West a mapping would only be called a fibration if it satisfied some suitable condition, for example, the homotopy lifting property for cubes ( "Serre fibration" ; see Covering homotopy for the homotopy lifting property, [a3]). A mapping would be called a morphism (respectively, an isomorphism) only if the induced function 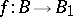were continuous (respectively, a homeomorphism).

References

[a1]	A. Dold, "Partitions of unity in the theory of fibrations" Ann. of Math. , 78 (1963) pp. 223–255
[a2]	D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)
[a3]	J.-P. Serre, "Homologie singulière des èspaces fibrés" Ann. of Math. , 54 (1951) pp. 425–505
[a4]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. Chapt. 2
[a5]	N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951)