Fibre product of objects in a category
A special case of the concept of an (inverse or projective) limit. Let  be a category and let
be a category and let  and
and  be given morphisms in
be given morphisms in  . An object
. An object  , together with morphisms
, together with morphisms  ,
,  , is called a fibre product of the objects
, is called a fibre product of the objects  and
and  (over
(over 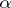 and
and 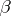 ) if
) if 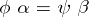 , and if for any pair of morphisms
, and if for any pair of morphisms 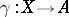 ,
,  for which
for which 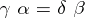 there exists a unique morphism
there exists a unique morphism  such that
such that 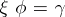 ,
, 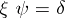 . The commutative square
. The commutative square
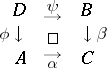 |
is often called a universal or Cartesian square. The object 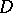 , together with the morphisms
, together with the morphisms 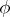 and
and 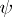 , is a limit of the diagram
, is a limit of the diagram
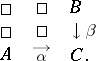 |
The fibre product of 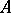 and
and  over
over 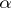 and
and  is written as
is written as
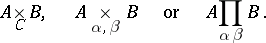 |
If it exists, the fibre product is uniquely defined up to an isomorphism.
In a category with finite products and kernels of pairs of morphisms, the fibre product of 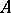 and
and  over
over 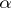 and
and 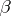 is formed as follows. Let
is formed as follows. Let 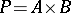 be the product of
be the product of 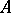 and
and 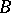 with projections
with projections 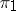 and
and 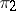 and let
and let 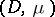 be the kernel of the pair of morphisms
be the kernel of the pair of morphisms 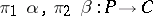 . Then
. Then 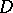 , together with the morphisms
, together with the morphisms  and
and  , is a fibre product of
, is a fibre product of 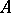 and
and  over
over 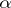 and
and  . In many categories of structured sets,
. In many categories of structured sets, 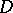 is the subset of
is the subset of 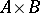 consisting of all those pairs
consisting of all those pairs  for which
for which 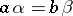 .
.
Comments
In the literature on category theory, fibre products are most commonly called pullbacks, and examples of the dual notion (i.e. fibre products in the opposite of the category under consideration) are called pushouts. The name "fibre product" derives from the fact that, in the category of sets (and hence, in any concrete category whose underlying-set functor preserves pullbacks), the fibre of  over an element
over an element 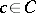 (i.e. the inverse image of
(i.e. the inverse image of  under the mapping
under the mapping 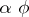 ) is the Cartesian product of the fibres
) is the Cartesian product of the fibres 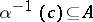 and
and 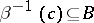 . Note also that (binary) products (cf. Product of a family of objects in a category) are a special case of pullbacks, in which the object
. Note also that (binary) products (cf. Product of a family of objects in a category) are a special case of pullbacks, in which the object 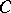 is taken to be a final object of the category.
is taken to be a final object of the category.
References
| [a1] | B. Mitchell, "Theory of categories" , Acad. Press (1965) |
| [a2] | J. Adámek, "Theory of mathematical structures" , Reidel (1983) |
Fibre product of objects in a category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fibre_product_of_objects_in_a_category&oldid=13216