Fibonacci numbers
The elements of the sequence  given by the initial values
given by the initial values  and the recurrence relation
and the recurrence relation  . The first 14 Fibonacci numbers were produced for the first time in 1228 in the manuscripts of Leonardo da Pisa (Fibonacci).
. The first 14 Fibonacci numbers were produced for the first time in 1228 in the manuscripts of Leonardo da Pisa (Fibonacci).
Operations that can be performed on the indices of the Fibonacci numbers can be reduced to operations on the numbers themselves. The basis for this lies in the "addition formula" :
 |
Immediate corollaries of it are:
 |
etc. The general "multiplication formula" is more complicated:
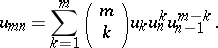 |
The elementary divisibility properties of the Fibonacci numbers are mainly determined by the following facts:  ; if
; if  is a prime number of the form
is a prime number of the form  , then
, then 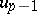 is divisible by
is divisible by 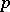 , while if it is of the form
, while if it is of the form  , then
, then  is; if
is; if 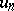 is divisible by a prime number
is divisible by a prime number  and if
and if 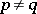 , then
, then  is not divisible by
is not divisible by 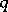 ; if
; if 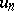 is divisible by a prime number
is divisible by a prime number  , then
, then  is divisible by
is divisible by 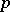 , but not by
, but not by  ; if
; if  is divisible by 4, then
is divisible by 4, then  is divisible by 2, but not by 4; if
is divisible by 2, but not by 4; if 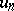 is divisible by 2 but not by 4, then
is divisible by 2 but not by 4, then  is divisible by 4, but not by 8. At the same time, some number-theoretic problems connected with Fibonacci numbers are extremely hard. For example, the question of whether the set of prime Fibonacci numbers is finite or not has not been solved (1984).
is divisible by 4, but not by 8. At the same time, some number-theoretic problems connected with Fibonacci numbers are extremely hard. For example, the question of whether the set of prime Fibonacci numbers is finite or not has not been solved (1984).
An important role in the theory of Fibonacci numbers is played by the number 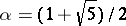 , which is a root of the equation
, which is a root of the equation 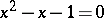 . Thus Binet's formula
. Thus Binet's formula
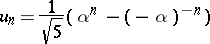 |
holds; it implies that 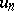 is the nearest integer to
is the nearest integer to  , and that
, and that
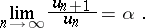 |
The Fibonacci numbers occupy a special position in the theory of continued fractions. In the continued-fraction expansion of  all the partial quotients are ones and the number of them is not less than that of the incomplete quotients of the expansion of any other fraction with denominator less than
all the partial quotients are ones and the number of them is not less than that of the incomplete quotients of the expansion of any other fraction with denominator less than  . In a certain sense the number
. In a certain sense the number 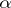 is described by its approximating fractions
is described by its approximating fractions  in a "worst possible" way.
in a "worst possible" way.
References
| [1] | B. Boncompagni, "Illiber Abbaci di Leonardo Pisano" , Rome (1857) |
| [2] | N.N. Vorob'ev, "Fibonacci numbers" , Moscow (1984) (In Russian) |
| [3] | V.E. Hoggatt, "Fibonacci and Lucas numbers" , Univ. Santa Clara (1969) |
| [4] | U. (or A. Brousseau) Alfred, "An introduction to Fibonacci discovery" , San José, CA (1965) |
| [5] | Fibonacci Quart. (1963-) |
Comments
Let 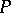 ,
,  be non-zero integers with
be non-zero integers with  and
and  . A Lucas sequence, or a sequence of Lucas numbers, is defined by
. A Lucas sequence, or a sequence of Lucas numbers, is defined by 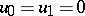 and the linear recurrence relation
and the linear recurrence relation
 |
Still more generally, a sequence  of complex numbers, i.e. a number-theoretic or arithmetic function, is said to be recurrent of order
of complex numbers, i.e. a number-theoretic or arithmetic function, is said to be recurrent of order  if there is a complex-valued function
if there is a complex-valued function 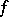 of
of  variables such that
variables such that 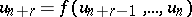 ,
,  . If
. If  is linear,
is linear, 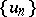 is called a linear recurrent sequence. Both the Fibonacci and the Lucas numbers are linearly recurrent of order 2.
is called a linear recurrent sequence. Both the Fibonacci and the Lucas numbers are linearly recurrent of order 2.
For some more results on Fibonacci numbers, Lucas numbers and recurrent sequences, as well as for their manifold applications, cf. also [a1].
References
| [a1] | A.N. Phillipou (ed.) G.E. Bergum (ed.) A.F. Horodam (ed.) , Fibonacci numbers and their applications , Reidel (1986) |
Fibonacci numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fibonacci_numbers&oldid=12076