Fermat theorem
From Encyclopedia of Mathematics
A necessary condition for a local extremum of a real-valued function. Suppose that a real-valued function 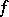 is defined in a neighbourhood of a point
is defined in a neighbourhood of a point 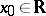 and is differentiable at that point. If
and is differentiable at that point. If 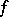 has a local extremum at
has a local extremum at  , then its derivative at
, then its derivative at 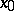 is equal to zero:
is equal to zero: 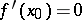 . Geometrically this means that the tangent to the graph of
. Geometrically this means that the tangent to the graph of  at the point
at the point  is horizontal. A condition equivalent to this for extrema of polynomials was first obtained by P. Fermat in 1629, but it was not published until 1679.
is horizontal. A condition equivalent to this for extrema of polynomials was first obtained by P. Fermat in 1629, but it was not published until 1679.
Comments
For Fermat's theorems in number theory see Fermat great theorem; Fermat little theorem.
How to Cite This Entry:
Fermat theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fermat_theorem&oldid=18337
Fermat theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fermat_theorem&oldid=18337
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article