Fermat-Torricelli problem
Torricelli–Fermat problem
The (generalized) Fermat–Torricelli problem, incorrectly also called the Steiner–Weber problem, refers to finding the unique point  ,
,  , minimizing the function
, minimizing the function
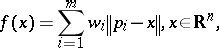 | (a1) |
for a set  of
of  given non-collinear points with corresponding positive weights
given non-collinear points with corresponding positive weights  , where
, where  denotes the Euclidean norm.
denotes the Euclidean norm.
In 1638, R. Descartes invited P. de Fermat to investigate (for  ) curves of the form
) curves of the form
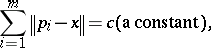 | (a2) |
which led Fermat to ask in 1643 for the minimum point with respect to the unweighted subcase  of (a1) (i.e.,
of (a1) (i.e.,  ), cf. [a14], p. 153. The first solution to this subcase was obtained by E. Torricelli (see [a29], [a30]) using the focal property of the ellipse, and further ruler-and-compass constructions were given by B. Cavalieri, V. Viviani, Th. Simpson, and H. Lebesgue; the unweighted case
), cf. [a14], p. 153. The first solution to this subcase was obtained by E. Torricelli (see [a29], [a30]) using the focal property of the ellipse, and further ruler-and-compass constructions were given by B. Cavalieri, V. Viviani, Th. Simpson, and H. Lebesgue; the unweighted case 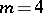 was solved by G. Fagnano, cf. [a34], [a20], and [a2], Chap. II, for extensive historical discussions and corrections. With the help of Galois theory it was proved in [a6] and [a1] that for
was solved by G. Fagnano, cf. [a34], [a20], and [a2], Chap. II, for extensive historical discussions and corrections. With the help of Galois theory it was proved in [a6] and [a1] that for 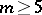 points in general position the Fermat–Torricelli problem does not allow exact algorithms under computation models with arithmetic operations and extraction of
points in general position the Fermat–Torricelli problem does not allow exact algorithms under computation models with arithmetic operations and extraction of  th roots. On the other hand,
th roots. On the other hand,  -approximative solutions for
-approximative solutions for 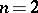 can be constructed in polynomial time, see [a4]. The weighted case
can be constructed in polynomial time, see [a4]. The weighted case 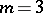 was completely solved by W. Launhardt [a21]; its relations to generalizations of the Napoleon theorem (also for higher dimensions) were investigated in [a24]. In 1846, E. Fasbender [a13] proved that the unweighted case
was completely solved by W. Launhardt [a21]; its relations to generalizations of the Napoleon theorem (also for higher dimensions) were investigated in [a24]. In 1846, E. Fasbender [a13] proved that the unweighted case 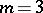 of minimizing (a1) is dual to the construction of the largest equilateral triangle circumscribed to the triangle
of minimizing (a1) is dual to the construction of the largest equilateral triangle circumscribed to the triangle  , and H.W. Kuhn [a19] pointed out that this Vecten–Fasbender duality is historically the first example of dualizing a problem in the spirit of non-linear programming.
, and H.W. Kuhn [a19] pointed out that this Vecten–Fasbender duality is historically the first example of dualizing a problem in the spirit of non-linear programming.
For  , the level curves (a2) of the function (a1) (with equal weights) are called poly-ellipses or multifocal ellipses. They were first studied by E.W. von Tschirnhaus [a31], who extended the classical gardener's string construction from
, the level curves (a2) of the function (a1) (with equal weights) are called poly-ellipses or multifocal ellipses. They were first studied by E.W. von Tschirnhaus [a31], who extended the classical gardener's string construction from  in (a2) to
in (a2) to 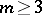 . Many further properties and applications of these curves (and of their analogues in the weighted and higher-dimensional situation) are collected in [a25], [a12] and [a16].
. Many further properties and applications of these curves (and of their analogues in the weighted and higher-dimensional situation) are collected in [a25], [a12] and [a16].
Analytic approaches to the minimum point 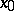 of (a1) were presented by J. Bertrand, R. Sturm, L.L. Lindelöf, Kuhn, C. Witzgall, and many others; in modern terms they can be summarized by the following theorem (see, e.g., [a18]):
of (a1) were presented by J. Bertrand, R. Sturm, L.L. Lindelöf, Kuhn, C. Witzgall, and many others; in modern terms they can be summarized by the following theorem (see, e.g., [a18]):
I) The minimum point  of (a1) exists and is unique.
of (a1) exists and is unique.
II) If for each  ,
,
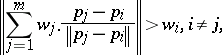 |
holds, then  and
and
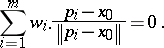 |
III) If there is a point  satisfying
satisfying
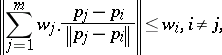 |
then  .
.
These characterizations of 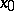 have a realistic appeal, since (for
have a realistic appeal, since (for  ) there is even a mechanical device based on the so-called Varignon frame: A board is drilled with
) there is even a mechanical device based on the so-called Varignon frame: A board is drilled with 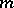 holes at the points
holes at the points 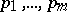 ;
; 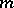 strings are tied together in a knot at one end, the loose ends are passed through the
strings are tied together in a knot at one end, the loose ends are passed through the 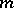 holes and are attached to physical weights below the board. The equilibrium position of the knot yields the solution. This was presented by G. Pick in [a32], Math. Appendix, but the early history of this approach is discussed in [a15].
holes and are attached to physical weights below the board. The equilibrium position of the knot yields the solution. This was presented by G. Pick in [a32], Math. Appendix, but the early history of this approach is discussed in [a15].
The first algorithmic approach to  was provided by E. Weiszfeld [a33], see also [a18]. It is gradient descent but not convergent at the foci
was provided by E. Weiszfeld [a33], see also [a18]. It is gradient descent but not convergent at the foci 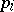 (cf. also Gradient method). L.M. Ostresh [a27] proposed the first completely convergent iteration procedure, which can even be applied in Banach spaces, see [a11].
(cf. also Gradient method). L.M. Ostresh [a27] proposed the first completely convergent iteration procedure, which can even be applied in Banach spaces, see [a11].
The Fermat–Torricelli problem has been one of the starting points of location science from operations research, in particular belonging to the field of continuous location theory, where it is usually called the  -median problem or single facility location problem, cf. [a8], [a22], and from the historical point of view also [a21], [a32] (see also Weber problem).
-median problem or single facility location problem, cf. [a8], [a22], and from the historical point of view also [a21], [a32] (see also Weber problem).
Since local conditions for Steiner points in Steiner minimal trees (cf. also Steiner tree problem; Steiner point) are based on properties of Fermat–Torricelli points, a related passage in [a7], pp. 354–361, can be considered as starting point of investigations in this direction (although the respective question goes back even to C.F. Gauss, 1836: To connect four towns by a network of minimal total length). For historical corrections with respect to Steiner minimal trees (including the fact that even the name is not justified, analogous to the wrong phrase "Steiner–Weber problem" instead of "Fermat–Torricelli problem" ) see [a20] and [a2], Sect. 23.9; a modern treatment of Steiner minimal trees is [a5].
Generalizations.
Generalizations of the problem to minimize (a1) were mainly studied in two directions.
Extensions to finite-dimensional normed spaces  (i.e., Minkowski spaces) or other non-Euclidean spaces: For example, denoting by
(i.e., Minkowski spaces) or other non-Euclidean spaces: For example, denoting by 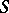 the (in Minkowski spaces not necessarily point-shaped) solution set, the property
the (in Minkowski spaces not necessarily point-shaped) solution set, the property 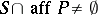 holds for all finite point sets
holds for all finite point sets  ,
,  , if and only if
, if and only if 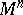 is an inner product space [a9]. Various further properties of
is an inner product space [a9]. Various further properties of 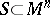 were investigated in [a10], see also [a3]. Extensions to other non-Euclidean spaces are considered in [a11], [a26].
were investigated in [a10], see also [a3]. Extensions to other non-Euclidean spaces are considered in [a11], [a26].
Modification of the given geometric configuration: For example, replacing the searched point in (a1) by a hyperplane 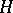 , one gets the median hyperplane problem (also called linear fit problem, or
, one gets the median hyperplane problem (also called linear fit problem, or  regression problem), which can be formulated with respect to vertical and orthogonal distances. The importance of this problem (e.g., compared with the known least-squares regression) for robust statistics is based on the fact that
regression problem), which can be formulated with respect to vertical and orthogonal distances. The importance of this problem (e.g., compared with the known least-squares regression) for robust statistics is based on the fact that 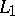 estimates are technically robust against arbitrary outliers, cf. [a28]. Also, such problems are studied in linear approximation theory and computational geometry (also in relation to the
estimates are technically robust against arbitrary outliers, cf. [a28]. Also, such problems are studied in linear approximation theory and computational geometry (also in relation to the  -set problem). Position criteria for median hyperplanes of weighted point sets and algorithmical approaches are presented in [a17] (for Euclidean
-set problem). Position criteria for median hyperplanes of weighted point sets and algorithmical approaches are presented in [a17] (for Euclidean  -spaces) and in [a23] (for other Minkowski
-spaces) and in [a23] (for other Minkowski  -spaces).
-spaces).
References
| [a1] | C. Bajaj, "The algebraic degree of geometric optimization problems." Discr. Comput. Geom. , 3 (1988) pp. 177–191 |
| [a2] | V. Boltyanski, H. Martini, V. Soltan, "Geometric methods and optimization problems" , Kluwer Acad. Publ. (1999) |
| [a3] | G.D. Chakerian, M.A. Ghandehari, "The Fermat problem in Minkowski spaces." Geom. Dedicata , 17 (1985) pp. 227–238 |
| [a4] | R. Chandrasekaran, A. Tamir, "Algebraic optimization: The Fermat–Weber problem" Math. Programming , 46 (1990) pp. 219–224 |
| [a5] | D. Cieslik, "Steiner minimal trees" , Kluwer Acad. Publ. (1999) |
| [a6] | E.J. Cockayne, Z.A. Melzak, "Euclidean constructibility in graph-minimization problems" Math. Mag. , 42 (1969) pp. 206–208 |
| [a7] | R. Courant, H. Robbins, "What is mathematics?" , Oxford Univ. Press (1941) |
| [a8] | "Facility location: A survey on applications and methods" Z. Drezner (ed.) , Ser. in Operations Research , Springer (1995) |
| [a9] | R. Durier, "The Fermat–Weber problem and inner product spaces" J. Approx. Th. , 78 (1994) pp. 161–173 |
| [a10] | R. Durier, C. Michelot, "Geometrical properties of the Fermat–Weber problem" European J. Oper. Res. , 20 (1985) pp. 332–343 |
| [a11] | U. Eckhardt, "Weber's problem and Weiszfeld's algorithm in general spaces" Math. Programming , 18 (1980) pp. 186–196 |
| [a12] | P. Erdös, I. Vincze, "On the approximation of convex, closed plane curves by multifocal ellipses" J. Appl. Probab. , 19A (1982) pp. 89–96 |
| [a13] | E. Fasbender, "Über die gleichseitigen Dreiecke, welche um ein gegebenes Dreieck gelegt werden können" J. Reine Angew. Math. , 30 (1846) pp. 230–231 |
| [a14] | P. de Fermat, "Œvres" , I , H. Tannery (ed.), Paris (1891) (Supplement: Paris 1922) |
| [a15] | O.I. Franksen, I. Gratan–Guinness, "The earliest contribution to location theory? Spatio-economic equilibrium with Lamé and Clapeyron (1829)" Math. and Computers in Simulation , 31 (1989) pp. 195–220 |
| [a16] | C. Gross, T.-K. Strempel, "On generalizations of conics and on a generalization of the Fermat–Torricelli point" Amer. Math. Monthly , 105 (1998) pp. 732–743 |
| [a17] | N.M. Korneenko, H. Martini, "Hyperplane approximation and related topics" J. Pach (ed.) , New Trends in Discrete and Computational Geometry , Springer (1993) pp. 135–162 |
| [a18] | H.W. Kuhn, "Steiner's problem revisited" G.B. Dantzig (ed.) B.C. Eaves (ed.) , Studies in Optimization , Studies in Math. , 10 , Math. Assoc. Amer. (1974) pp. 52–70 |
| [a19] | H.W. Kuhn, "Nonlinear programming: A historical view" R.W. Cottle (ed.) C.W. Lemke (ed.) , SIAM–AMS Proc. , 9 , Amer. Math. Soc. (1976) pp. 1–26 |
| [a20] | Y.S. Kupitz, H. Martini, "Geometric aspects of the generalized Fermat–Torricelli problem" I. Básrásny (ed.) K. Böröczky (ed.) , Intuitive Geometry (Budapest, 1995) , 6 , Bolyai Soc. Math. Studies (1997) pp. 55–127 |
| [a21] | W. Launhardt, "Kommercielle Tracirung der Verkehrswege" , Hannover (1872) |
| [a22] | R.F. Love, J.G. Morris, G.O. Wesolowsky, "Facilities location: models and methods" , North-Holland (1988) |
| [a23] | H. Martini, A. Schöbel, "Median hyperplanes in normed spaces — a survey" Discr. Appl. Math. , 89 (1998) pp. 181–195 |
| [a24] | H. Martini, B. Weissbach, "Napoleon's theorem with weights in  -space" Geom. Dedicata , 74 (1999) pp. 213–223 -space" Geom. Dedicata , 74 (1999) pp. 213–223 |
| [a25] | Z.A. Melzak, J.S. Forsyth, "Polyconics 1: Polyellipses and optimization" Quart. Appl. Math. , 35 (1977) pp. 239–255 |
| [a26] | R. Noda, T. Sakai, M. Morimoto, "Generalized Fermat's problem." Canad. Math. Bull. , 34 (1991) pp. 96–104 |
| [a27] | L.M. Ostresh, "On the convergence of a class of iterative methods for solving the Weber location problem" Operat. Res. , 26 (1978) pp. 597–609 |
| [a28] | P.J. Rousseeuw, A.M. Leroy, "Robust regression and outlier detection" , Wiley (1987) |
| [a29] | E. Torricelli, "Opere" , I/2 , Faënza (1919) pp. 90–97 |
| [a30] | E. Torricelli, "Opere" , III , Faënza (1919) pp. 426–431 |
| [a31] | E.W. von Tschirnhaus, "Medicina mentis" , Lipsiae (1695) (German ed. by R. Zaunick, Acta Historica Leopoldina, J.A. Barth, Leipzig 1963) |
| [a32] | A. Weber, "Über den Standort der Industrien, Teil I: Reine Theorie des Standorts" , J.C.B. Mohr, Tübingen (1909) (English ed. by C.J. Friedrichs, Univ. Chicago Press, 1929) |
| [a33] | E. Weiszfeld, "Sur le point pour lequel la somme des distances de  points donnés est minimu" Tôhoku Math. J. , 43 (1937) pp. 355–386 points donnés est minimu" Tôhoku Math. J. , 43 (1937) pp. 355–386 |
| [a34] | G.O. Wesolowsky, "The Weber problem — history and perspectives" J. Location Sci. , 1 (1993) pp. 5–23 |
Fermat-Torricelli problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fermat-Torricelli_problem&oldid=22419