Fermat-Goss-Denis theorem
Fermat's last theorem is the claim that  has no solutions in non-zero integers for
has no solutions in non-zero integers for  (see also Fermat last theorem). However, over a function field
(see also Fermat last theorem). However, over a function field  (cf. also Algebraic function), with
(cf. also Algebraic function), with  of non-zero characteristic
of non-zero characteristic  , the appropriate generalization is not just to take
, the appropriate generalization is not just to take  ,
,  and
and  as polynomials over
as polynomials over  in
in 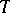 . In any event, in characteristic zero, or for
. In any event, in characteristic zero, or for  prime to the characteristic
prime to the characteristic 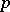 , it is fairly easy to see, by descent on the degrees of a putative solution
, it is fairly easy to see, by descent on the degrees of a putative solution 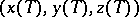 , that there is not even a non-trivial solution over
, that there is not even a non-trivial solution over 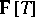 , with
, with 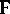 the algebraic closure of
the algebraic closure of 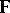 .
.
In 1982, D. Goss [a1] formulated a suitable analogue for the case  . Goss notes that, traditionally, Fermat's equation is viewed as
. Goss notes that, traditionally, Fermat's equation is viewed as 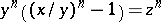 , where the connection with cyclotomic fields, and thence the classical exponential function, is displayed: the zeros of
, where the connection with cyclotomic fields, and thence the classical exponential function, is displayed: the zeros of 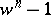 are precisely the
are precisely the  roots of unity. But in characteristic
roots of unity. But in characteristic 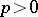 the analogue of the exponential function comes by way of the Drinfel'd module; more specifically, the Carlitz module. A familiar and elementary manifestation of such things is the Hilbert theorem 90, whereby a cyclic extension of degree
the analogue of the exponential function comes by way of the Drinfel'd module; more specifically, the Carlitz module. A familiar and elementary manifestation of such things is the Hilbert theorem 90, whereby a cyclic extension of degree 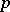 in characteristic
in characteristic 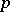 is not given by a zero of
is not given by a zero of 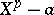 , but of
, but of 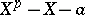 .
.
Let  be the field of
be the field of 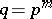 elements. The equation that in this context appears to raise issues analogous to those provoked by the classical Fermat equation is
elements. The equation that in this context appears to raise issues analogous to those provoked by the classical Fermat equation is
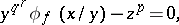 |
where 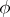 is the Carlitz module determined by
is the Carlitz module determined by  and
and  denotes the Frobenius mapping relative to
denotes the Frobenius mapping relative to 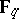 , i.e. the mapping that gives
, i.e. the mapping that gives  powers. To say that
powers. To say that 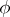 is the Carlitz module is to require also that
is the Carlitz module is to require also that 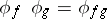 . Goss [a1] deals, à la Kummer, with the case of this equation when
. Goss [a1] deals, à la Kummer, with the case of this equation when  is a regular prime of
is a regular prime of  .
.
The equation has two important parameters, the element 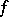 of
of 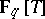 and the order
and the order 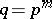 . As usual, a solution with
. As usual, a solution with 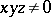 is called non-trivial. When
is called non-trivial. When 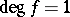 , Goss shows that in analogy with the equation
, Goss shows that in analogy with the equation  there are an infinity of solutions. Suppose
there are an infinity of solutions. Suppose 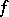 is monic. L. Denis [a2] proves that if
is monic. L. Denis [a2] proves that if 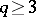 ,
, 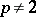 and
and  , there is no non-trivial solution. If
, there is no non-trivial solution. If 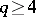 ,
, 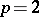 and
and  , there is a unique solution proportional in
, there is a unique solution proportional in 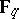 to the triplet
to the triplet 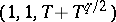 in the case
in the case 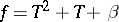 , where
, where 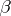 is a square in
is a square in 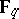 ; and if
; and if  ,
, 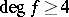 , then there is a solution only if
, then there is a solution only if 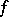 is of the shape
is of the shape 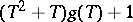 , and it is
, and it is 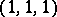 . Denis deals completely with the remaining cases
. Denis deals completely with the remaining cases  . Because
. Because 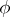 is
is 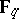 -linear, one can now easily produce the results for
-linear, one can now easily produce the results for 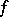 not monic.
not monic.
In settling the general case, Denis [a2] speaks of the Fermat–Goss theorem. It seems appropriate here to write of the Fermat–Goss–Denis theorem.
References
| [a1] | D. Goss, "On a Fermat equation arising in the arithmetic theory of function fields" Math. Ann. , 261 (1982) pp. 269–286 |
| [a2] | L. Denis, "Le théorème de Fermat–Goss" Trans. Amer. Math. Soc. , 343 (1994) pp. 713–726 |
Fermat-Goss-Denis theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fermat-Goss-Denis_theorem&oldid=16667