Fefferman-Garsia inequality
C. Fefferman [a3] discovered the remarkable fact that the space 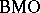 is none other than the "dual" of the Hardy space
is none other than the "dual" of the Hardy space 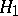 in the sense of function analysis (cf. also Functional analysis; Hardy spaces; Duality;
in the sense of function analysis (cf. also Functional analysis; Hardy spaces; Duality; 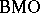 -space). In establishing the above duality, Fefferman discovered the following "formal" inequality: if
-space). In establishing the above duality, Fefferman discovered the following "formal" inequality: if 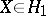 and
and 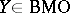 , then
, then
 |
The word "formal" is used here since 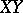 does not necessarily have a finite Lebesgue integral. However, one can define
does not necessarily have a finite Lebesgue integral. However, one can define 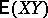 by setting
by setting  , since it has been proved that in this case
, since it has been proved that in this case 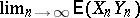 exists. Here,
exists. Here, 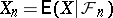 and
and 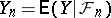 ,
, 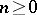 ,
, 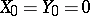 a.s., are regular martingales. Later, A.M. Garsia [a4] proved an analogous inequality for
a.s., are regular martingales. Later, A.M. Garsia [a4] proved an analogous inequality for 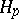 with
with 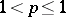 .
.
S. Ishak and J. Mogyorodi [a5] extended the validity of the Fefferman–Garsia inequality to all 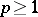 . In 1983, [a6], [a7], [a8], they also proved the following generalization: If
. In 1983, [a6], [a7], [a8], they also proved the following generalization: If 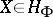 and
and 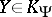 , where
, where 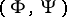 is a pair of conjugate Young functions (cf. also Dual functions) such that
is a pair of conjugate Young functions (cf. also Dual functions) such that 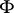 has a finite power, then
has a finite power, then
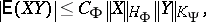 |
where 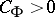 is a constant depending only on
is a constant depending only on 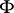 and
and 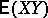 stands for
stands for 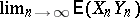 , which exists.
, which exists.
It was proved in [a1], [a2] that the generalized Fefferman–Garsia inequality holds if and only if the right-hand side of the corresponding Burkholder–Davis–Gundy inequality holds.
References
| [a1] | N.L. Bassily, "Approximation theory" , Proc. Conf. Kecksemet, Hungary, 1990 , Colloq. Math. Soc. Janos Bolyai , 58 (1991) pp. 85–96 |
| [a2] | N.L. Bassily, "Probability theory and applications. Essays in memory of J. Mogyorodi" Math. Appl. , 80 (1992) pp. 33–45 |
| [a3] | C. Fefferman, "Characterisation of bounded mean oscillation" Amer. Math. Soc. , 77 (1971) pp. 587–588 |
| [a4] | A.M. Garsia, "Martingale inequalities. Seminar notes on recent progress" , Mathematics Lecture Notes , Benjamin (1973) |
| [a5] | S. Ishak, J. Mogyorodi, "On the generalization of the Fefferman–Garsia inequality" , Proc. 3rd IFIP-WG17/1 Working Conf. , Lecture Notes in Control and Information Science , 36 , Springer (1981) pp. 85–97 |
| [a6] | S. Ishak, J. Mogyorodi, "On the 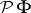 -spaces and the generalization of Herz's and Fefferman inequalities I" Studia Math. Hung. , 17 (1982) pp. 229–234 -spaces and the generalization of Herz's and Fefferman inequalities I" Studia Math. Hung. , 17 (1982) pp. 229–234 |
| [a7] | S. Ishak, J. Mogyorodi, "On the 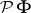 -spaces and the generalization of Herz's and Fefferman inequalities II" Studia Math. Hung. , 18 (1983) pp. 205–210 -spaces and the generalization of Herz's and Fefferman inequalities II" Studia Math. Hung. , 18 (1983) pp. 205–210 |
| [a8] | S. Ishak, J. Mogyorodi, "On the 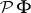 -spaces and the generalization of Herz's and Fefferman inequalities III" Studia Math. Hung. , 18 (1983) pp. 211–219 -spaces and the generalization of Herz's and Fefferman inequalities III" Studia Math. Hung. , 18 (1983) pp. 211–219 |
Fefferman-Garsia inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fefferman-Garsia_inequality&oldid=17021