Difference between revisions of "Fefferman-Garsia inequality"
Ulf Rehmann (talk | contribs) m (moved Fefferman–Garsia inequality to Fefferman-Garsia inequality: ascii title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | f1100401.png | ||
| + | $#A+1 = 26 n = 3 | ||
| + | $#C+1 = 26 : ~/encyclopedia/old_files/data/F110/F.1100040 Fefferman\ANDGarsia inequality | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | C. Fefferman [[#References|[a3]]] discovered the remarkable fact that the space $ { \mathop{\rm BMO} } $ | |
| + | is none other than the "dual" of the Hardy space $ H _ {1} $ | ||
| + | in the sense of function analysis (cf. also [[Functional analysis|Functional analysis]]; [[Hardy spaces|Hardy spaces]]; [[Duality|Duality]]; [[BMO-space| $ { \mathop{\rm BMO} } $- | ||
| + | space]]). In establishing the above duality, Fefferman discovered the following "formal" inequality: if $ X \in H _ {1} $ | ||
| + | and $ Y \in { \mathop{\rm BMO} } $, | ||
| + | then | ||
| − | + | $$ | |
| + | \left | { {\mathsf E} ( XY ) } \right | \leq c \left \| X \right \| _ {H _ {1} } \left \| Y \right \| _ { { \mathop{\rm BMO} } } . | ||
| + | $$ | ||
| − | + | The word "formal" is used here since $ XY $ | |
| + | does not necessarily have a finite [[Lebesgue integral|Lebesgue integral]]. However, one can define $ {\mathsf E} ( XY ) $ | ||
| + | by setting $ {\mathsf E} ( XY ) = {\lim\limits } _ {n \rightarrow \infty } {\mathsf E} ( X _ {n} Y _ {n} ) $, | ||
| + | since it has been proved that in this case $ {\lim\limits } _ {n \rightarrow \infty } {\mathsf E} ( X _ {n} Y _ {n} ) $ | ||
| + | exists. Here, $ X _ {n} = {\mathsf E} ( X \mid {\mathcal F} _ {n} ) $ | ||
| + | and $ Y _ {n} = {\mathsf E} ( Y \mid {\mathcal F} _ {n} ) $, | ||
| + | $ n \geq 0 $, | ||
| + | $ X _ {0} = Y _ {0} = 0 $ | ||
| + | a.s., are regular martingales. Later, A.M. Garsia [[#References|[a4]]] proved an analogous inequality for $ H _ {p} $ | ||
| + | with $ 1 < p \leq 1 $. | ||
| − | + | S. Ishak and J. Mogyorodi [[#References|[a5]]] extended the validity of the Fefferman–Garsia inequality to all $ p \geq 1 $. | |
| + | In 1983, [[#References|[a6]]], [[#References|[a7]]], [[#References|[a8]]], they also proved the following generalization: If $ X \in H _ \Phi $ | ||
| + | and $ Y \in K _ \Psi $, | ||
| + | where $ ( \Phi, \Psi ) $ | ||
| + | is a pair of conjugate Young functions (cf. also [[Dual functions|Dual functions]]) such that $ \Phi $ | ||
| + | has a finite power, then | ||
| + | |||
| + | $$ | ||
| + | \left | { {\mathsf E} ( XY ) } \right | \leq C _ \Phi \left \| X \right \| _ {H _ \Phi } \left \| Y \right \| _ {K _ \Psi } , | ||
| + | $$ | ||
| + | |||
| + | where $ C _ \Phi > 0 $ | ||
| + | is a constant depending only on $ \Phi $ | ||
| + | and $ {\mathsf E} ( XY ) $ | ||
| + | stands for $ {\lim\limits } _ {n \rightarrow \infty } {\mathsf E} ( X _ {n} Y _ {n} ) $, | ||
| + | which exists. | ||
It was proved in [[#References|[a1]]], [[#References|[a2]]] that the generalized Fefferman–Garsia inequality holds if and only if the right-hand side of the corresponding [[Burkholder–Davis–Gundy inequality|Burkholder–Davis–Gundy inequality]] holds. | It was proved in [[#References|[a1]]], [[#References|[a2]]] that the generalized Fefferman–Garsia inequality holds if and only if the right-hand side of the corresponding [[Burkholder–Davis–Gundy inequality|Burkholder–Davis–Gundy inequality]] holds. | ||
Revision as of 19:38, 5 June 2020
C. Fefferman [a3] discovered the remarkable fact that the space $ { \mathop{\rm BMO} } $
is none other than the "dual" of the Hardy space $ H _ {1} $
in the sense of function analysis (cf. also Functional analysis; Hardy spaces; Duality; $ { \mathop{\rm BMO} } $-
space). In establishing the above duality, Fefferman discovered the following "formal" inequality: if $ X \in H _ {1} $
and $ Y \in { \mathop{\rm BMO} } $,
then
$$ \left | { {\mathsf E} ( XY ) } \right | \leq c \left \| X \right \| _ {H _ {1} } \left \| Y \right \| _ { { \mathop{\rm BMO} } } . $$
The word "formal" is used here since $ XY $ does not necessarily have a finite Lebesgue integral. However, one can define $ {\mathsf E} ( XY ) $ by setting $ {\mathsf E} ( XY ) = {\lim\limits } _ {n \rightarrow \infty } {\mathsf E} ( X _ {n} Y _ {n} ) $, since it has been proved that in this case $ {\lim\limits } _ {n \rightarrow \infty } {\mathsf E} ( X _ {n} Y _ {n} ) $ exists. Here, $ X _ {n} = {\mathsf E} ( X \mid {\mathcal F} _ {n} ) $ and $ Y _ {n} = {\mathsf E} ( Y \mid {\mathcal F} _ {n} ) $, $ n \geq 0 $, $ X _ {0} = Y _ {0} = 0 $ a.s., are regular martingales. Later, A.M. Garsia [a4] proved an analogous inequality for $ H _ {p} $ with $ 1 < p \leq 1 $.
S. Ishak and J. Mogyorodi [a5] extended the validity of the Fefferman–Garsia inequality to all $ p \geq 1 $. In 1983, [a6], [a7], [a8], they also proved the following generalization: If $ X \in H _ \Phi $ and $ Y \in K _ \Psi $, where $ ( \Phi, \Psi ) $ is a pair of conjugate Young functions (cf. also Dual functions) such that $ \Phi $ has a finite power, then
$$ \left | { {\mathsf E} ( XY ) } \right | \leq C _ \Phi \left \| X \right \| _ {H _ \Phi } \left \| Y \right \| _ {K _ \Psi } , $$
where $ C _ \Phi > 0 $ is a constant depending only on $ \Phi $ and $ {\mathsf E} ( XY ) $ stands for $ {\lim\limits } _ {n \rightarrow \infty } {\mathsf E} ( X _ {n} Y _ {n} ) $, which exists.
It was proved in [a1], [a2] that the generalized Fefferman–Garsia inequality holds if and only if the right-hand side of the corresponding Burkholder–Davis–Gundy inequality holds.
References
| [a1] | N.L. Bassily, "Approximation theory" , Proc. Conf. Kecksemet, Hungary, 1990 , Colloq. Math. Soc. Janos Bolyai , 58 (1991) pp. 85–96 |
| [a2] | N.L. Bassily, "Probability theory and applications. Essays in memory of J. Mogyorodi" Math. Appl. , 80 (1992) pp. 33–45 |
| [a3] | C. Fefferman, "Characterisation of bounded mean oscillation" Amer. Math. Soc. , 77 (1971) pp. 587–588 |
| [a4] | A.M. Garsia, "Martingale inequalities. Seminar notes on recent progress" , Mathematics Lecture Notes , Benjamin (1973) |
| [a5] | S. Ishak, J. Mogyorodi, "On the generalization of the Fefferman–Garsia inequality" , Proc. 3rd IFIP-WG17/1 Working Conf. , Lecture Notes in Control and Information Science , 36 , Springer (1981) pp. 85–97 |
| [a6] | S. Ishak, J. Mogyorodi, "On the 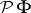 -spaces and the generalization of Herz's and Fefferman inequalities I" Studia Math. Hung. , 17 (1982) pp. 229–234 -spaces and the generalization of Herz's and Fefferman inequalities I" Studia Math. Hung. , 17 (1982) pp. 229–234 |
| [a7] | S. Ishak, J. Mogyorodi, "On the 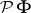 -spaces and the generalization of Herz's and Fefferman inequalities II" Studia Math. Hung. , 18 (1983) pp. 205–210 -spaces and the generalization of Herz's and Fefferman inequalities II" Studia Math. Hung. , 18 (1983) pp. 205–210 |
| [a8] | S. Ishak, J. Mogyorodi, "On the 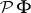 -spaces and the generalization of Herz's and Fefferman inequalities III" Studia Math. Hung. , 18 (1983) pp. 211–219 -spaces and the generalization of Herz's and Fefferman inequalities III" Studia Math. Hung. , 18 (1983) pp. 211–219 |
Fefferman-Garsia inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fefferman-Garsia_inequality&oldid=46910