Favard measure
of order  of a subset
of a subset  in a Euclidean space
in a Euclidean space  of dimension
of dimension 
A generalization of the Hausdorff measure; it was introduced by J. Favard [1]. The precise definition is: The group of motions of  induces on the collection of its
induces on the collection of its  -dimensional affine subspaces a left-invariant Haar measure
-dimensional affine subspaces a left-invariant Haar measure  that is unique up to normalization, and the set
that is unique up to normalization, and the set  induces a function
induces a function  the value of which at an affine subspace
the value of which at an affine subspace  is the number of points in the intersection
is the number of points in the intersection 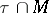 . The Favard measure of
. The Favard measure of 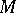 is the value of
is the value of  at
at 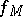 , if the normalizing constant is chosen so that
, if the normalizing constant is chosen so that 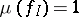 for the
for the 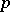 -dimensional unit cube
-dimensional unit cube 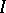 .
.
The Favard measure of order 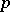 of a set
of a set 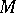 does not exceed its Hausdorff
does not exceed its Hausdorff 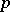 -measure
-measure 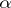 and, in the case when
and, in the case when  , it is the same as
, it is the same as 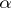 if and only if
if and only if 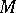 splits into a countable number of parts one of which has Hausdorff
splits into a countable number of parts one of which has Hausdorff 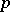 -measure zero and each of the others can be situated on a smooth
-measure zero and each of the others can be situated on a smooth 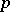 -dimensional manifold.
-dimensional manifold.
References
| [1] | J. Favard, "Une définition de la longueur et de l'aire" C.R. Acad. Sci. Paris , 194 (1932) pp. 344–346 |
| [2] | H. Federer, "Geometric measure theory" , Springer (1969) |
Favard measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Favard_measure&oldid=13597