Fatou arc

for a meromorphic function in a domain of the complex -plane

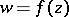An accessible boundary arc (cf. Attainable boundary arc) of with the property that it forms part of the boundary of some Jordan domain in which , , is bounded. Sometimes this definition is broadened, replacing the condition that is bounded in by the more general condition that the image of under the mapping is not dense in the 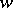-plane. The strengthened version of Fatou's theorem in the theory of boundary properties of analytic functions asserts that if is a Fatou arc (even in the extended sense) for a function that is meromorphic in the disc 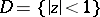, then at almost-every point , has a finite limit as tends to from inside 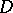within any angle with vertex formed by a pair of chords of .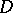

References

[1]	E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6
[2]	I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)
[3]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)