Fano surface
From Encyclopedia of Mathematics
The surface parametrized by the family of lines lying on a non-singular cubic surface 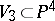 . G. Fano studied the family of lines
. G. Fano studied the family of lines 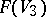 on a three-dimensional cubic [1].
on a three-dimensional cubic [1].
Through a generic point of a non-singular cubic  there pass exactly 6 lines lying on it, and the Fano surface
there pass exactly 6 lines lying on it, and the Fano surface 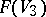 is a non-singular irreducible reduced algebraic surface of geometric genus
is a non-singular irreducible reduced algebraic surface of geometric genus 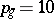 and irregularity
and irregularity 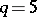 , with topological Euler characteristic (in case
, with topological Euler characteristic (in case 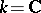 ) equal to 27. From the Fano surface
) equal to 27. From the Fano surface 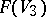 one can reconstruct the cubic
one can reconstruct the cubic 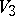 (see [2]).
(see [2]).
References
| [1] | G. Fano, "Sul sisteme 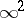 di rette contenuto in une varietà cubica generale dello spacio a quattro dimensioni" Atti R. Accad. Sci. Torino , 39 (1903–1904) pp. 778–792 di rette contenuto in une varietà cubica generale dello spacio a quattro dimensioni" Atti R. Accad. Sci. Torino , 39 (1903–1904) pp. 778–792 |
| [2] | A.N. [A.N. Tyurin] Tjurin, "On the Fano surface of a nonsingular cubic in 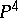 " Math. USSR Izv. , 4 : 6 (1960) pp. 1207–1214 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 6 (1970) pp. 1200–1208 " Math. USSR Izv. , 4 : 6 (1960) pp. 1207–1214 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 6 (1970) pp. 1200–1208 |
| [3] | C. Clemens, P. Griffiths, "The intermediate Jacobian of the cubic threefold" Ann. of Math. , 95 (1972) pp. 281–356 |
How to Cite This Entry:
Fano surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fano_surface&oldid=11261
Fano surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fano_surface&oldid=11261
This article was adapted from an original article by Vik.S. Kulikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article