Faddeev-Popov ghost
An auxiliary field, not physical and known as a ghost field, which was introduced in the quantization procedure of non-Abelian gauge theories.
The quantization procedure of non-Abelian gauge theories demands the introduction of certain auxiliary fields, known as ghosts fields, which are not physical. The need for such fields was first observed by R. Feynman [a6], based on unitary arguments. Later, the quantization procedure of Yang–Mills theory (cf. also Yang–Mills field) based on a path integral (functional integral) was developed by L.D. Faddeev and V.N. Popov [a5], and this procedure as a whole is known as the Faddeev–Popov method. Faddeev–Popov ghosts (anti-ghosts) are fictitious anti-commuting complex scalar fields 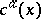 (respectively,
(respectively, 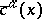 ), where
), where 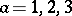 and
and  is a point of the space-time, which are used in the Faddeev–Popov method to represent the Faddeev–Popov determinant appearing in the generating functional of the
is a point of the space-time, which are used in the Faddeev–Popov method to represent the Faddeev–Popov determinant appearing in the generating functional of the 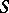 -matrix in the form of a fermionic Gaussian integral (Berezin integral). If
-matrix in the form of a fermionic Gaussian integral (Berezin integral). If 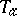 ,
, 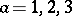 , are the generators of the Lie algebra
, are the generators of the Lie algebra 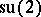 , then the Faddeev–Popov ghosts (anti-ghosts) are usually combined into the Lie algebra
, then the Faddeev–Popov ghosts (anti-ghosts) are usually combined into the Lie algebra 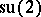 -valued function
-valued function 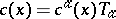 (respectively,
(respectively, 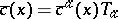 ). Although the Faddeev–Popov ghosts anti-commute, they are not physical fermionic fields.
). Although the Faddeev–Popov ghosts anti-commute, they are not physical fermionic fields.
From a mathematical point of view, the Faddeev–Popov ghosts are the generators of the infinite-dimensional Grassmann algebra, whose description can be found in [a3]. It follows from the structure of an infinite-dimensional Grassmann algebra that the Faddeev–Popov ghosts satisfy the following commutation relations:
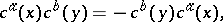 | (a1) |
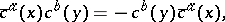 | (a2) |
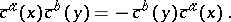 | (a3) |
The introduction of Faddeev–Popov ghosts leads to the appearance of additional terms in the exponent of the generating functional; these terms are combined with the classical Yang–Mills Lagrangian into the quantum Lagrangian. It turns out that the quantum Lagrangian is invariant under the Becchi–Rouet–Stora–Tyutin transformations 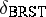 (BRST transformations; cf. [a2], [a10]), which are nilpotent:
(BRST transformations; cf. [a2], [a10]), which are nilpotent:  , i.e. applied twice to any field they give zero. Later, the BRST transformations
, i.e. applied twice to any field they give zero. Later, the BRST transformations  were complemented by the anti-BRST transformations
were complemented by the anti-BRST transformations  [a9], which are also nilpotent.
[a9], which are also nilpotent.
It is well known that an appropriate geometric framework for the Yang–Mills theory is the theory of connections on fibre bundles (cf. also Connection; Principal fibre bundle). This fact and the nilpotency of the BRST transformations suggested an idea to construct a geometric interpretation for the Faddeev–Popov ghosts and BRST transformations in terms of exterior differentiation and differential forms on a principal fibre bundle (cf. also Exterior algebra). A first geometric interpretation of this kind, identifying the Faddeev–Popov ghost  with a Lie algebra-valued
with a Lie algebra-valued 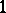 -form on a principal bundle, was proposed by Y. Ne'eman and J. Thierry-Mieg [a8]. In order to incorporate the anti-ghost
-form on a principal bundle, was proposed by Y. Ne'eman and J. Thierry-Mieg [a8]. In order to incorporate the anti-ghost  and anti-BRST transformations into this geometric Ne'eman–Thierry-Mieg interpretation, the formalism of
and anti-BRST transformations into this geometric Ne'eman–Thierry-Mieg interpretation, the formalism of 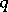 -vector fields, considered as
-vector fields, considered as 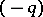 -forms, and a corresponding analogue of exterior differentiation was developed by Ü. Lumiste [a7]. A geometric interpretation of the Faddeev–Popov ghost
-forms, and a corresponding analogue of exterior differentiation was developed by Ü. Lumiste [a7]. A geometric interpretation of the Faddeev–Popov ghost  and anti-ghost
and anti-ghost  , identifying them with the components of a connection form on a super fibre bundle, was proposed by L. Bonora and M. Tonin [a4] and was subsequently specified by Lumiste in [a7].
, identifying them with the components of a connection form on a super fibre bundle, was proposed by L. Bonora and M. Tonin [a4] and was subsequently specified by Lumiste in [a7].
It should be noted that all geometric interpretations of the Faddeev–Popov ghosts mentioned above lay aside the structure of infinite-dimensional Grassmann algebra (a1)–(a3) generated by the ghosts and anti-ghosts. In other words, identification of the Fadeev–Popov ghost  with a differential form leads to anti-commutative behaviour of ghosts only with respect to superscripts:
with a differential form leads to anti-commutative behaviour of ghosts only with respect to superscripts: 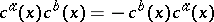 , but not in different points of the space-time. The infinite-dimensional structure of the Grassmann algebra generated by the Faddeev–Popov ghosts was used in [a1] to construct an infinite-dimensional super-manifold with underlying infinite-dimensional manifold of all connections of a principal fibre bundle. In this approach, the Faddeev–Popov ghosts play the role of odd coordinates of a super-manifold. It was shown that the quantum Lagrangian, considered as a function on an infinite-dimensional super-manifold, can be obtained by a procedure of continuation of the classical Yang–Mills Lagrangian from the underlying manifold of all connections to the super-manifold.
, but not in different points of the space-time. The infinite-dimensional structure of the Grassmann algebra generated by the Faddeev–Popov ghosts was used in [a1] to construct an infinite-dimensional super-manifold with underlying infinite-dimensional manifold of all connections of a principal fibre bundle. In this approach, the Faddeev–Popov ghosts play the role of odd coordinates of a super-manifold. It was shown that the quantum Lagrangian, considered as a function on an infinite-dimensional super-manifold, can be obtained by a procedure of continuation of the classical Yang–Mills Lagrangian from the underlying manifold of all connections to the super-manifold.
The Faddeev–Popov ghosts allow one to develop a BRST method of quantization based on the BRST transformations. This method was later used in quantization of several field theories. It also plays an essential role in developing topological field theories in dimension four [a11].
References
| [a1] | V. Abramov, Ü. Lumiste, "Superspace with underlying Banach fiber bundle of connections and the supersymmetries of effective action" Soviet Math. (Iz. VUZ) , 30 : 1 (1986) pp. 1–13 |
| [a2] | C. Becchi, A. Rouet, R. Stora, Commun. Math. Phys. , 42 (1975) pp. 127 |
| [a3] | F.A. Berezin, "The method of second quantization" , Acad. Press (1966) |
| [a4] | L. Bonora, M. Tonin, "Superfield formulation of extended BRS symmetry" Phys. Lett. , 98B (1981) pp. 48–50 |
| [a5] | L.D. Faddeev, V.N. Popov, Phys. Lett. , B25 (1967) pp. 29 |
| [a6] | R.P. Feynman, Acta Physica Polonica , 24 (1963) pp. 697 |
| [a7] | Ü. Lumiste, "Connections in geometric interpretation of Yang–Mills and Faddeev–Popov fields" Soviet Math. (Iz. VUZ) , 27 : 1 (1983) pp. 51–62 |
| [a8] | Y. Ne'eman, J. Thierry-Mieg, "Geometrical gauge theory of ghost and Goldstone fields and of ghost symmetries" Proc. Nat. Acad. Sci. USA , 77 : 2 (1980) pp. 720–723 |
| [a9] | I. Ojima, "Another BRS transformation" Progr. Theoret. Phys. , 64 : 2 (1980) pp. 625–638 |
| [a10] | I.V. Tyutin, Preprint PhIAN , 39 (1975) |
| [a11] | E. Witten, "Topological quantum field theory" Comm. Math. Phys. , 117 (1988) pp. 353–386 |
Faddeev-Popov ghost. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Faddeev-Popov_ghost&oldid=15367