Factorial ring
A ring with unique decomposition into factors. More precisely, a factorial ring 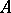 is an integral domain in which one can find a system of irreducible elements
is an integral domain in which one can find a system of irreducible elements 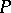 such that every non-zero element
such that every non-zero element 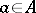 admits a unique representation
admits a unique representation
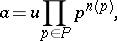 |
where  is invertible and the non-negative integral exponents
is invertible and the non-negative integral exponents 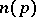 are non-zero for only a finite number of elements
are non-zero for only a finite number of elements 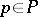 . Here an element is called irreducible in
. Here an element is called irreducible in 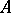 if
if 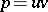 implies that either
implies that either  or
or  is invertible in
is invertible in 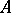 , and
, and 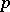 is not invertible in
is not invertible in 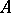 .
.
In a factorial ring there is a highest common divisor and a least common multiple of any two elements. A ring 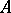 is factorial if and only if it is a Krull ring and satisfies one of the following equivalent conditions: 1) every divisorial ideal of
is factorial if and only if it is a Krull ring and satisfies one of the following equivalent conditions: 1) every divisorial ideal of 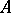 is principal; 2) every prime ideal of height 1 is principal; and 3) every non-empty family of principal ideals has a maximal element, and the intersection of any two principal ideals is principal. Every principal ideal ring is factorial. A Dedekind ring is factorial only if it is a principal ideal ring. If
is principal; 2) every prime ideal of height 1 is principal; and 3) every non-empty family of principal ideals has a maximal element, and the intersection of any two principal ideals is principal. Every principal ideal ring is factorial. A Dedekind ring is factorial only if it is a principal ideal ring. If 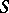 is a multiplicative system in a factorial ring
is a multiplicative system in a factorial ring 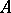 , then the ring of fractions
, then the ring of fractions 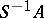 is factorial. A Zariski ring
is factorial. A Zariski ring 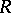 is factorial if its completion
is factorial if its completion 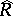 is.
is.
Subrings and quotient rings of a factorial ring need not be factorial. The ring of polynomials over a factorial ring and the ring of formal power series over a field or over a discretely-normed ring are factorial. But the ring of formal power series over a factorial ring need not be factorial.
An integral domain is factorial if and only if its multiplicative semi-group is Gaussian (see Gauss semi-group), and for this reason factorial rings are also called Gaussian rings or Gauss rings.
References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
Comments
For the notion of height see Height of an ideal.
A Zariski ring is a Noetherian ring 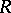 having an ideal
having an ideal  such that every ideal in
such that every ideal in 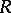 is closed in the
is closed in the  -adic topology (cf. Adic topology). The last condition can be replaced by: Every element
-adic topology (cf. Adic topology). The last condition can be replaced by: Every element  for which
for which 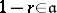 is invertible in
is invertible in 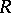 . A Zariski ring
. A Zariski ring 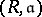 is complete if it is a complete topological space (in the
is complete if it is a complete topological space (in the  -adic topology). The completion of a Zariski ring
-adic topology). The completion of a Zariski ring 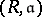 is the completion of the topological space
is the completion of the topological space 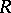 (in the
(in the  -adic topology). This completion,
-adic topology). This completion, 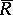 , is a Zariski ring (take
, is a Zariski ring (take 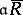 as ideal).
as ideal).
Factorial ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Factorial_ring&oldid=15956