Factorial
The function defined on the set of non-negative integers with value at  equal to the product of the natural numbers from 1 to
equal to the product of the natural numbers from 1 to  , that is, to
, that is, to  ; it is denoted by
; it is denoted by  (by definition,
(by definition,  ). For large
). For large  an approximate expression for the factorial is given by the Stirling formula. The factorial is equal to the number of permutations of
an approximate expression for the factorial is given by the Stirling formula. The factorial is equal to the number of permutations of  elements. The more general expression
elements. The more general expression
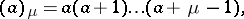 |
is also called a factorial, where  is a complex number,
is a complex number, 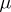 is a natural number, and
is a natural number, and 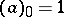 . See also Gamma-function.
. See also Gamma-function.
Comments
Because  equals the number of permutations of
equals the number of permutations of  elements, the factorial is extensively used in combinatorics, probability theory, mathematical statistics, etc. Cf. Combinatorial analysis; Combination; Binomial coefficients.
elements, the factorial is extensively used in combinatorics, probability theory, mathematical statistics, etc. Cf. Combinatorial analysis; Combination; Binomial coefficients.
Factorial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Factorial&oldid=18764