Factor algebra
An involutive subalgebra 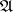 of the algebra
of the algebra  of linear operators on a Hilbert space
of linear operators on a Hilbert space 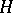 that is closed relative to so-called weak convergence of operators and has the property that its centre (that is, the collection of all operators in
that is closed relative to so-called weak convergence of operators and has the property that its centre (that is, the collection of all operators in 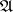 that commute with every operator in
that commute with every operator in 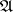 ) consists of scalar multiples of the unit operator.
) consists of scalar multiples of the unit operator.
If 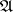 is a factor, then for a large supply of subspaces
is a factor, then for a large supply of subspaces 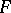 of
of  one can define the concept of the dimension
one can define the concept of the dimension 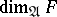 relative to
relative to 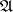 as an invariant that is preserved, not under arbitrary isometries
as an invariant that is preserved, not under arbitrary isometries 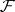 , but only under those in the given factor with additional natural properties (for example,
, but only under those in the given factor with additional natural properties (for example, 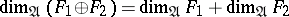 ). All factors can be divided into five classes corresponding to the values that
). All factors can be divided into five classes corresponding to the values that 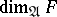 can take, where, for example, for a factor of class
can take, where, for example, for a factor of class 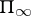 it can take any value in
it can take any value in  .
.
Comments
An involutive algebra is an algebra over 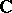 endowed with an involution. For information concerning various types of factors cf. von Neumann algebra.
endowed with an involution. For information concerning various types of factors cf. von Neumann algebra.
References
| [a1] | G.K. Pedersen, "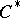 -algebras and their automorphism groups" , Acad. Press (1979) -algebras and their automorphism groups" , Acad. Press (1979) |
| [a2] | J. Dixmier, "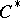 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Factor algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Factor_algebra&oldid=11524