Exterior product
A fundamental operation in the exterior algebra of tensors defined on an  -dimensional vector space
-dimensional vector space  over a field
over a field  .
.
Let  be a basis of
be a basis of  , and let
, and let  and
and  be
be  - and
- and  -forms:
-forms:
 |
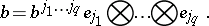 |
The exterior product of the forms  and
and 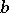 is the
is the 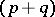 -form
-form  obtained by alternation of the tensor product
obtained by alternation of the tensor product 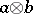 . The form
. The form  is denoted by
is denoted by 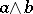 ; its coordinates are skew-symmetric:
; its coordinates are skew-symmetric:
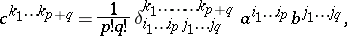 |
where 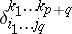 are the components of the generalized Kronecker symbol. The exterior product of covariant tensors is defined in a similar manner.
are the components of the generalized Kronecker symbol. The exterior product of covariant tensors is defined in a similar manner.
The basic properties of the exterior product are listed below:
1) 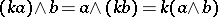 ,
, 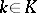 (homogeneity);
(homogeneity);
2)  (distributivity);
(distributivity);
3) 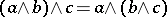 (associativity).
(associativity).
4)  ; if the characteristic of
; if the characteristic of 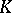 is distinct from two, the equation
is distinct from two, the equation 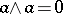 is valid for any form
is valid for any form  of odd valency.
of odd valency.
The exterior product of  vectors is said to be a decomposable
vectors is said to be a decomposable  -vector. Any poly-vector of dimension
-vector. Any poly-vector of dimension  is a linear combination of decomposable
is a linear combination of decomposable  -vectors. The components of this combination are the (
-vectors. The components of this combination are the (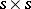 )-minors of the (
)-minors of the (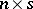 )-matrix
)-matrix 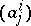 ,
, 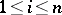 ,
, 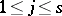 , of the coefficients of the vectors
, of the coefficients of the vectors  . If
. If  their exterior product has the form
their exterior product has the form
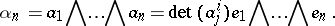 |
Over fields of characteristic distinct from two, the equation 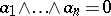 is necessary and sufficient for vectors
is necessary and sufficient for vectors  to be linearly dependent. A non-zero decomposable
to be linearly dependent. A non-zero decomposable  -vector
-vector 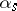 defines in
defines in  an
an  -dimensional oriented subspace
-dimensional oriented subspace 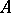 , parallel to the vectors
, parallel to the vectors  , and the parallelotope in
, and the parallelotope in 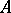 formed by the vectors
formed by the vectors  issuing from one point, denoted by
issuing from one point, denoted by 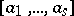 . The conditions
. The conditions 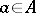 and
and 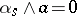 are equivalent.
are equivalent.
For references see Exterior algebra.
Comments
Instead of exterior product the phrase "outer product" is sometimes used. The condition 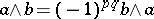 for
for  of degree
of degree 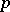 and
and 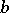 of degree
of degree 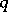 is sometimes called graded commutativity.
is sometimes called graded commutativity.
Exterior product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Exterior_product&oldid=31347