Exterior and interior boundary value problems
Boundary value problems for elliptic partial differential equations in the finite (interior) domain 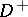 , respectively in the infinite (exterior) domain
, respectively in the infinite (exterior) domain 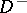 into which a given closed smooth surface
into which a given closed smooth surface 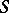 , homeomorphic to a sphere, subdivides the Euclidean space
, homeomorphic to a sphere, subdivides the Euclidean space 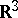 .
.
The principal difference between exterior and interior boundary value problems consists in the fact that in the former case the boundary condition must be supplemented by a stipulation as to a certain behaviour at infinity, which ensures that the solution is unique and which is natural from the point of view of the physical origin of the problem itself.
For instance, in the exterior boundary value problems for the Poisson equation 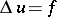 (the function
(the function 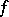 is assumed to be sufficiently smooth and of compact support) it is sufficient to stipulate that the solution
is assumed to be sufficiently smooth and of compact support) it is sufficient to stipulate that the solution 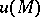 be regular at infinity, i.e. that
be regular at infinity, i.e. that
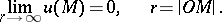 | (1) |
In the case of the Poisson equation 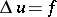 in an infinite domain in the plane,
in an infinite domain in the plane, 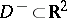 , the regularity condition at infinity is reduced to stipulating that the solution
, the regularity condition at infinity is reduced to stipulating that the solution 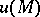 be bounded at infinity:
be bounded at infinity:
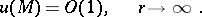 | (2) |
In the case of the exterior boundary value problem for the Helmholtz equation 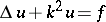 ,
, 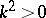 , the stipulation of regularity at infinity proves to be insufficient to obtain a unique solution. Here the so-called radiation conditions are employed. For the domain
, the stipulation of regularity at infinity proves to be insufficient to obtain a unique solution. Here the so-called radiation conditions are employed. For the domain 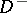 in
in 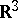 :
:
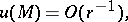 | (3) |
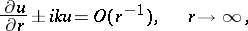 |
and for  :
:
 | (4) |
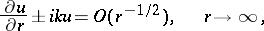 |
the signs being chosen depending on the conditions of the problem and the choice of a principal fundamental solution. About other conditions at infinity see Limit-absorption principle; Limiting-amplitude principle.
Consider a boundary value problem for a linear elliptic equation of general form
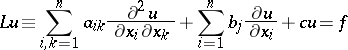 | (5) |
in the domains 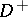 and
and 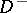 of the Euclidean space
of the Euclidean space 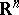 ,
, 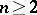 , separated by a closed smooth hypersurface
, separated by a closed smooth hypersurface 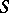 that is homeomorphic to the sphere in
that is homeomorphic to the sphere in 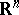 , the functions
, the functions 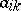 ,
, 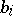 ,
,  , and
, and 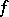 being assumed sufficiently smooth, and
being assumed sufficiently smooth, and 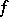 being of compact support. The conditions of regularity at infinity of type (1) or (2) will be sufficient in exterior boundary value problems if
being of compact support. The conditions of regularity at infinity of type (1) or (2) will be sufficient in exterior boundary value problems if 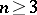 or
or 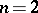 , if the maximum principle is satisfied by the operator
, if the maximum principle is satisfied by the operator  and if there exists a single unique principal fundamental solution; in particular, a necessary condition for it is
and if there exists a single unique principal fundamental solution; in particular, a necessary condition for it is 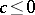 (see [1], [2], [3]). The problem of the applicability of the radiation conditions, the principle of limit absorption and the limiting-amplitude principle in their general form has not yet (1977) been exhaustively investigated.
(see [1], [2], [3]). The problem of the applicability of the radiation conditions, the principle of limit absorption and the limiting-amplitude principle in their general form has not yet (1977) been exhaustively investigated.
In addition to the difference between the conditions at infinity, an exterior and interior boundary value problem may also differ by the conditions for existence of the solution. Thus, in the case of the interior Neumann problem for the Laplace equation 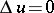 in a finite domain
in a finite domain 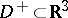 , a necessary condition for the existence of a solution has the form
, a necessary condition for the existence of a solution has the form
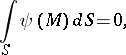 |
where  is the given boundary function in the Neumann condition
is the given boundary function in the Neumann condition 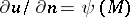 . However, this condition is no longer necessary in the exterior Neumann problem in an infinite domain
. However, this condition is no longer necessary in the exterior Neumann problem in an infinite domain 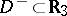 .
.
References
| [1] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
| [2] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
| [3] | V.D. Kupradze, "Randwertaufgaben der Schwingungstheorie und Integralgleichungen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [4] | V.D. Kupradze, "The method of potentials in elasticity theory" , Moscow (1963) (In Russian) |
| [5] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
Comments
References
| [a1] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [a2] | F. John, "Partial differential equations" , Springer (1971) |
| [a3] | P.R. Garabedian, "Partial differential equations" , Wiley (1964) |
| [a4] | I.G. Petrovskii, "Partial differential equations" , Saunders (1967) (Translated from Russian) |
Exterior and interior boundary value problems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Exterior_and_interior_boundary_value_problems&oldid=13211