Extension theorems
Theorems on the continuation (extension) of functions from one set to a larger set in such a way that the extended function satisfies certain definite properties. Problems on the analytic continuation of functions are, first of all, related to extension theorems.
An example of a theorem on the existence of a continuous extension of a continuous function is the Brouwer–Urysohn theorem: If 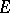 is a closed subset of a normal space
is a closed subset of a normal space  and
and 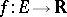 is a continuous real-valued bounded function, then there exists a continuous bounded function
is a continuous real-valued bounded function, then there exists a continuous bounded function 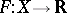 such that
such that 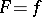 on
on 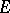 . The Hahn–Banach theorem on the extension of linear functionals in vector spaces is an extension theorem.
. The Hahn–Banach theorem on the extension of linear functionals in vector spaces is an extension theorem.
In a Euclidean space extension theorems are mainly related to the following two problems: 1) the extension of functions with domain properly belonging to a space onto the whole space; and 2) the extension of functions from the boundary to the entire domain. In both cases it is required that the extended function has definite smoothness properties, i.e. belongs to an appropriate class of functions, depending on the properties of the function to be extended.
The problem of extending functions from a domain with a sufficiently smooth boundary to the whole space while preserving continuity of the partial derivatives was solved by M.R. Hestenes [3] and H. Whitney . If functions  ,
,  , are given on the
, are given on the 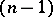 -dimensional boundary
-dimensional boundary  of a domain
of a domain 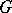 in the
in the  -dimensional space
-dimensional space 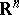 , then the problem of constructing a function
, then the problem of constructing a function 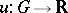 for which
for which
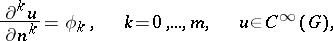 | (*) |
where  is the normal to
is the normal to 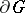 , has been considered by E.E. Levi [5], G. Giraud [6],
, has been considered by E.E. Levi [5], G. Giraud [6],
and M. Gevrey [8] in case the smoothness of the 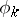 and of
and of 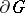 is described in terms of continuity and membership of a Hölder space (in the presence of, possibly, certain singularities). The order of growth of the partial derivatives of orders
is described in terms of continuity and membership of a Hölder space (in the presence of, possibly, certain singularities). The order of growth of the partial derivatives of orders  as the argument tends to the boundary
as the argument tends to the boundary 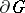 of
of 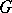 has also been studied.
has also been studied.
Both problems have been systematically studied by S.M. Nikol'skii and his students (cf. [9], [10]) in the cases of extension of functions in various  metrics
metrics 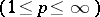 , in various variations and in various function spaces. Best characteristics of differentiability properties of functions that can be obtained from extending functions with given differentiability-difference properties have been found in terms of series of function spaces (cf. Imbedding theorems). Concerning the problem (*) one has found extensions that are optimal with respect to the order of growth of the derivatives of orders
, in various variations and in various function spaces. Best characteristics of differentiability properties of functions that can be obtained from extending functions with given differentiability-difference properties have been found in terms of series of function spaces (cf. Imbedding theorems). Concerning the problem (*) one has found extensions that are optimal with respect to the order of growth of the derivatives of orders 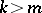 when approaching the boundary of the manifold (cf. [11], ).
when approaching the boundary of the manifold (cf. [11], ).
Often one substantiates methods for extending functions and systems of functions (*) from the boundary to the whole domain by integral representations. Usually, convenient methods for the extension of functions are linear. There are also other methods, e.g. based on expanding functions in series with subsequent extension of each term of the series. This method is, as a rule, non-linear. There are cases in which a linear method definitely does not exist, [13].
References
| [1] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [3] | M.R. Hestenes, "Extension of the range of differentiable functions" Duke Math. J. , 8 (1941) pp. 183–192 |
| [4a] | H. Whitney, "Analytic extension of differentiable functions defined in closed sets" Trans. Amer. Math. Soc. , 36 (1934) pp. 63–89 |
| [4b] | H. Whitney, "Differentiable functions defined in arbitrary subsets of Euclidean space" Trans. Amer. Math. Soc. , 40 (1936) pp. 309–317 |
| [5] | E.E. Levi, Mem. Soc. Itali XL , 16 (1909) pp. 3–112 |
| [6] | G. Giraud, "Sur le problème de Dirichlet généralisé" Ann. Sci. Ecole Norm. Sup. , 46 (1929) pp. 131–245 |
| [7a] | G. Giraud, "Sur certains problèmes non-linéaires de Neumann et sur certains problèmes non-linéaires mixtes" Ann. Sci. Ecole Norm. Sup. , 49 (1932) pp. 1–104 |
| [7b] | G. Giraud, "Sur certains problèmes non-linéaires de Neumann et sur certains problèmes non-linéaires mixtes" Ann. Sci. Ecole Norm. Sup. , 49 (1932) pp. 245–309 |
| [8] | M. Gevrey, "Les quasi-fonctions de Green et les systèmes d'équations aux dérivées partielles du type elliptique" Ann. Sci. Ecole Norm. Sup. , 52 (1935) pp. 39–108 |
| [9] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [10] | O.V. Besov, V.P. Il'in, S.M. Nikol'skii, "Integral representations of functions and imbedding theorems" , Wiley (1978) (Translated from Russian) |
| [11] | L.D. Kudryavtsev, Trudy Mat. Inst. Steklov. , 55 (1956) |
| [12a] | S.V. Uspenskii, "Inclusion and extension theorems for a class of functions" Siberian Math. J. , 7 : 1 (1966) pp. 154–161 Sibirsk. Mat. Zh. , 7 : 1 (1966) pp. 192–199 |
| [12b] | S.V. Uspenskii, "Embedding and extension theorems for one class of functions II" Siberian Math. J. , 7 : 2 (1966) pp. 333–342 Sibirsk. Mat. Zh. , 7 : 2 (1966) pp. 409–418 |
| [13] | N.I. Burenkov, M.L. Gol'dman, "On extension of 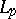 -functions" Proc. Steklov Inst. Math. , 150 (1967) pp. 33–54 Trudy Mat. Inst. Steklov. , 150 (1979) pp. 31–51 -functions" Proc. Steklov Inst. Math. , 150 (1967) pp. 33–54 Trudy Mat. Inst. Steklov. , 150 (1979) pp. 31–51 |
Comments
The Brouwer–Urysohn theorem is usually called the Tietze–Urysohn theorem or Tietze's extension theorem. It remains true if "bounded" is deleted twice.
Extension theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Extension_theorems&oldid=14119