Extension of an associative algebra

over a commutative ring

A homomorphism 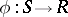of a -algebra onto . If is an algebra with zero multiplication, then the extension is called singular. In this case, is an -module in a natural way. The set of all extensions of with kernel 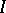admits an equivalence relation (the same as for groups, modules, etc.), and the set of equivalence classes of extensions is denoted by . If the algebra is -projective, then the algebra splits into a direct sum of 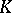-modules, 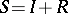, and the elements of can be written as pairs , , 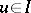, 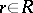with multiplication given by

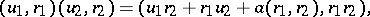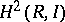where . The associativity of multiplication imposes restrictions on that make it into a cocycle. Mapping an extension to its cocycle defines an isomorphism of -modules between and the second cohomology group of 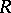with coefficients in .

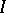In a completely different context, any algebra containing 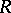is also called an extension of . Such extensions are often connected with a specific construction (polynomials over 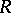, localization of 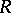, ring of partial fractions of the algebra 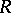, etc.). See also Extension of a field.

References

[1]	S. MacLane, "Homology" , Springer (1963)
[2]	G. Hochschild, "On the cohomology groups of an associative algebra" Ann. of Math. , 46 (1945) pp. 58–67

Comments

The cohomology group is also known as the Hochschild cohomology (group) of with values in .