Exponential mapping
A mapping of the tangent space of a manifold 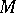 into
into  . It is defined by a connection given on
. It is defined by a connection given on 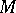 and is a far-reaching generalization of the ordinary exponential function regarded as a mapping of a straight line into itself.
and is a far-reaching generalization of the ordinary exponential function regarded as a mapping of a straight line into itself.
1) Let 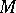 be a
be a 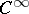 -manifold with an affine connection, let
-manifold with an affine connection, let 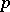 be a point in
be a point in 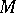 , let
, let 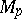 be the tangent space to
be the tangent space to 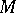 at
at 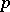 , let
, let 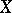 be a non-zero vector in
be a non-zero vector in 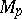 , and let
, and let 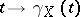 be the geodesic passing through
be the geodesic passing through 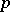 in the direction of
in the direction of 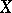 . There is an open neighbourhood
. There is an open neighbourhood 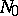 of the point
of the point  in
in 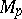 and an open neighbourhood
and an open neighbourhood 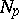 of
of 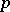 in
in 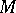 such that the mapping
such that the mapping 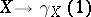 is a diffeomorphism of
is a diffeomorphism of 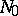 onto
onto 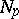 . This mapping is called the exponential mapping at
. This mapping is called the exponential mapping at 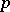 and is denoted by
and is denoted by 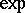 . A neighbourhood
. A neighbourhood 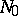 is called normal if: 1) the mapping
is called normal if: 1) the mapping  maps
maps 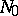 onto
onto 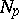 diffeomorphically; and 2)
diffeomorphically; and 2) 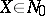 and
and 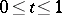 imply that
imply that 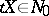 . In this case
. In this case 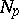 is said to be a normal neighbourhood of the point
is said to be a normal neighbourhood of the point 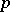 in the manifold
in the manifold  . Every
. Every 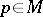 has a convex normal neighbourhood
has a convex normal neighbourhood 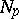 : Any two points of such a neighbourhood can be joined by exactly one geodesic segment lying in
: Any two points of such a neighbourhood can be joined by exactly one geodesic segment lying in 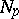 . If
. If 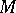 is a complete Riemannian manifold, then
is a complete Riemannian manifold, then 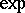 is a surjective mapping of
is a surjective mapping of 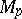 onto
onto 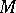 .
.
2) Let 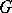 be a Lie group with identity
be a Lie group with identity  and let
and let 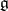 be the corresponding Lie algebra consisting of the tangent vectors to
be the corresponding Lie algebra consisting of the tangent vectors to 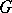 at
at  . For every vector
. For every vector 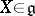 there is a unique differentiable homomorphism
there is a unique differentiable homomorphism 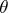 of the group
of the group 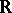 into
into 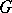 such that the tangent vector to
such that the tangent vector to 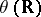 at
at  coincides with
coincides with 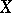 . The mapping
. The mapping 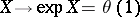 is called the exponential mapping of the algebra
is called the exponential mapping of the algebra 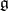 into the group
into the group 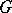 . There is an open neighbourhood
. There is an open neighbourhood 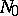 of the point
of the point  in
in 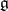 and an open neighbourhood
and an open neighbourhood 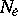 of
of  in
in 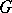 such that
such that 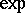 is a diffeomorphism of
is a diffeomorphism of 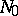 onto
onto 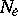 . Let
. Let 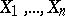 be some basis for the algebra
be some basis for the algebra 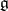 . The mapping
. The mapping 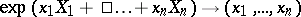 is a coordinate system on
is a coordinate system on 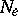 ; these coordinates are called canonical.
; these coordinates are called canonical.
The concept of an exponential mapping of a Lie group 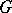 can also be approached from another point of view. There is a one-to-one correspondence between the set of all affine connections on
can also be approached from another point of view. There is a one-to-one correspondence between the set of all affine connections on 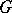 that are invariant relative to the group of left translations and the set of bilinear functions
that are invariant relative to the group of left translations and the set of bilinear functions 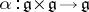 . It turns out that the exponential mapping
. It turns out that the exponential mapping  of the algebra
of the algebra 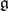 into the group
into the group 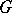 coincides with the mapping
coincides with the mapping 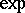 of the tangent space of
of the tangent space of 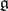 into the manifold
into the manifold 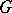 at the point
at the point  in this manifold with respect to the left-invariant affine connection corresponding to any skew-symmetric bilinear function
in this manifold with respect to the left-invariant affine connection corresponding to any skew-symmetric bilinear function 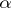 .
.
References
| [1] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
Exponential mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Exponential_mapping&oldid=12230