Exponential family of probability distributions
A certain model (i.e., a set of probability distributions on the same measurable space) in statistics which is widely used and studied for two reasons:
i) many classical models are actually exponential families;
ii) most of the classical methods of estimation of parameters and testing work successfully when the model is an exponential family.
The definitions found in the literature can be rather inelegant or lacking rigour. A mathematically satisfactory definition is obtained by first defining a significant particular case, namely the natural exponential family, and then using it to define general exponential families.
Given a finite-dimensional real linear space  , denote by
, denote by  the space of linear forms
the space of linear forms  from
from  to
to  . One writes
. One writes  instead of
instead of  . Let
. Let  be a positive measure on
be a positive measure on  (equipped with Borel sets), and assume that
(equipped with Borel sets), and assume that  is not concentrated on an affine hyperplane of
is not concentrated on an affine hyperplane of 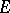 . Denote by
. Denote by
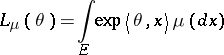 |
its Laplace transform and by 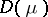 the subset of
the subset of 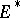 on which
on which 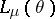 is finite. It is easily seen that
is finite. It is easily seen that 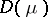 is convex. Assume that the interior
is convex. Assume that the interior 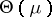 of
of 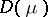 is not empty. The set of probability measures (cf. also Probability measure) on
is not empty. The set of probability measures (cf. also Probability measure) on 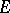 :
:
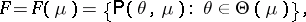 |
where
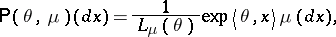 |
is called the natural exponential family (abbreviated NEF) generated by 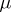 . The mapping
. The mapping
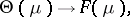 |
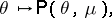 |
is called the canonical parametrization of 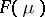 . A simple example of a natural exponential family is given by the family of binomial distributions
. A simple example of a natural exponential family is given by the family of binomial distributions 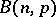 ,
, 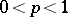 , with fixed parameter
, with fixed parameter  , generated by the measure
, generated by the measure
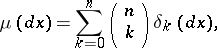 |
where 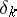 is the Dirac measure (cf. Measure) on
is the Dirac measure (cf. Measure) on 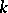 (cf. also Binomial distribution). Here, with
(cf. also Binomial distribution). Here, with  and
and 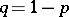 one has
one has
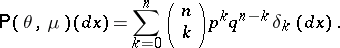 |
Note that the canonical parametrization by 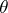 generally differs from a more familiar parametrization if the natural exponential family is a classical family. This is illustrated by the above example, where the parametrization by
generally differs from a more familiar parametrization if the natural exponential family is a classical family. This is illustrated by the above example, where the parametrization by 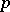 is traditional.
is traditional.
A general exponential family (abbreviated GEF) is defined on an abstract measure space 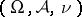 (the measure
(the measure  is not necessarily bounded) by a measurable mapping
is not necessarily bounded) by a measurable mapping 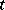 from
from  to a finite-dimensional real linear space
to a finite-dimensional real linear space 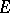 . This mapping
. This mapping 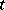 must have the following property: the image
must have the following property: the image 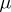 of
of  by
by 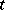 must be such that
must be such that 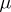 is not concentrated on an affine hyperplane of
is not concentrated on an affine hyperplane of 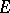 , and such that
, and such that 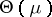 is not empty. Under these circumstances, the general exponential family on
is not empty. Under these circumstances, the general exponential family on  generated by
generated by 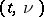 is:
is:
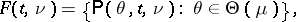 |
where
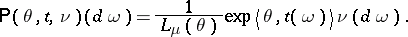 |
In this case, the NEF 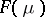 on
on 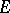 is said to be associated to the GEF
is said to be associated to the GEF 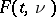 . In a sense, all results about GEFs are actually results about their associated NEF. The dimension of
. In a sense, all results about GEFs are actually results about their associated NEF. The dimension of 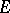 is called the order of the general exponential family.
is called the order of the general exponential family.
The most celebrated example of a general exponential family is the family of the normal distributions 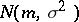 on
on 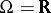 , where the mean
, where the mean 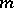 and the variance
and the variance 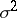 are both unknown parameters (cf. also Normal distribution). Here,
are both unknown parameters (cf. also Normal distribution). Here, 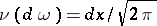 , the space
, the space 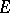 is
is 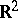 and
and 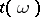 is
is 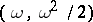 . Here, again, the canonical parametrization is not the classical one but is related to it by
. Here, again, the canonical parametrization is not the classical one but is related to it by 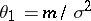 and
and 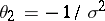 . The associated NEF is concentrated on a parabola in
. The associated NEF is concentrated on a parabola in 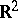 .
.
A common incorrect statement about such a model says that it belongs to "the" exponential family. Such a statement is induced by a confusion between a definite probability distribution and a family of them. When a NEF is concentrated on the set of non-negative integers, its elements are sometimes called "power series" distributions, since the Laplace transform is more conveniently written 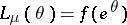 , where
, where 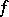 is analytic around
is analytic around  . The same confusion arises here.
. The same confusion arises here.
There are several variations of the above definition of a GEF: mostly, the parameter 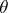 is taken to belong to
is taken to belong to 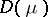 and not only to
and not only to 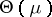 , thus obtaining what one may call a full-NEF. A full-GEF is similarly obtained. However, many results are not true anymore for such an extension: for instance, this is the case for the NEF on
, thus obtaining what one may call a full-NEF. A full-GEF is similarly obtained. However, many results are not true anymore for such an extension: for instance, this is the case for the NEF on 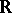 generated by a positive stable distribution
generated by a positive stable distribution 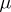 with parameter
with parameter 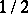 : this NEF is a family of inverse Gaussian distributions, with exponential moments, while
: this NEF is a family of inverse Gaussian distributions, with exponential moments, while 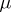 has no expectation and belongs to the full-NEF. A more genuine extension gives curved exponential families (abbreviated CEF). In this case, the set of parameters is restricted to a non-affine subset of
has no expectation and belongs to the full-NEF. A more genuine extension gives curved exponential families (abbreviated CEF). In this case, the set of parameters is restricted to a non-affine subset of 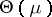 , generally a manifold. However, this extension is in a sense too general, since most of the models in statistics can be regarded as a CEF. The reason is the following: Starting from a statistical model of the form
, generally a manifold. However, this extension is in a sense too general, since most of the models in statistics can be regarded as a CEF. The reason is the following: Starting from a statistical model of the form 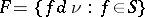 , where
, where 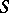 is a subset of
is a subset of 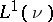 , then
, then 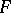 is a CEF if and only if the linear subspace of the space
is a CEF if and only if the linear subspace of the space 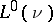 generated by the set
generated by the set 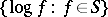 is finite dimensional. This is also why exponential families constructed on infinite-dimensional spaces are uninteresting (at least without further structure). For these CEFs, there are no really general results available concerning the application of the maximum-likelihood method. General references are [a2] and [a5].
is finite dimensional. This is also why exponential families constructed on infinite-dimensional spaces are uninteresting (at least without further structure). For these CEFs, there are no really general results available concerning the application of the maximum-likelihood method. General references are [a2] and [a5].
The exponential dispersion model (abbreviated, EDP) is a concept which is related to natural exponential families as follows: starting from the NEF 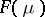 on
on 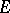 , the Jorgensen set
, the Jorgensen set 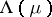 is the set of positive
is the set of positive 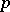 such that there exists a positive measure
such that there exists a positive measure 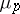 on
on 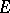 whose Laplace transform is
whose Laplace transform is 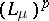 (see [a4]. Trivially, it contains all positive integers. The model
(see [a4]. Trivially, it contains all positive integers. The model
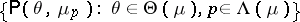 |
is the exponential dispersion model generated by 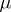 . It has the following striking property: Let
. It has the following striking property: Let 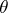 be fixed in
be fixed in 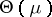 , let
, let  be in
be in 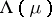 and let
and let  be independent random variables with respective distributions
be independent random variables with respective distributions  , with
, with  . Then the distribution of
. Then the distribution of 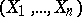 conditioned by
conditioned by 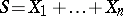 does not depend on
does not depend on  . The distribution of
. The distribution of 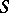 is obviously
is obviously 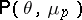 with
with  . Furthermore, if the parameters
. Furthermore, if the parameters  are known, and if
are known, and if 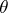 is unknown, then the maximum-likelihood method to estimate
is unknown, then the maximum-likelihood method to estimate 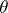 from the knowledge of the observations
from the knowledge of the observations 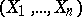 is the one obtained from the knowledge of
is the one obtained from the knowledge of 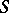 . For instance, if the NEF is the Bernoulli family of distributions
. For instance, if the NEF is the Bernoulli family of distributions 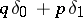 on
on  and
and 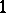 , if
, if 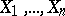 are independent Bernoulli random variables with the same unknown
are independent Bernoulli random variables with the same unknown 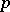 , then in order to estimate
, then in order to estimate 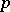 it is useless to keep track of the individual values of the
it is useless to keep track of the individual values of the 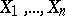 . All necessary information about
. All necessary information about 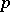 is contained in
is contained in 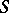 , which has a binomial distribution
, which has a binomial distribution 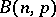 .
.
Thus, the problem of estimating the canonical parameter 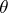 , given
, given  independent observations
independent observations 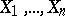 , for a NEF model is reduced to the problem of estimating with only one observation
, for a NEF model is reduced to the problem of estimating with only one observation 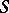 , whose distribution is in the NEF
, whose distribution is in the NEF 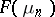 . See Natural exponential family of probability distributions for details about estimation by the maximum-likelihood method. When dealing with a GEF, the problem is reduced to the associated NEF.
. See Natural exponential family of probability distributions for details about estimation by the maximum-likelihood method. When dealing with a GEF, the problem is reduced to the associated NEF.
Bayesian theory (cf. also Bayesian approach) also constitutes a successful domain of application of exponential families. Given a NEF 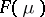 and a positive measure
and a positive measure 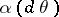 on
on 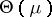 , consider the set of
, consider the set of 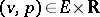 such that
such that
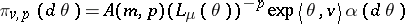 |
is a probability for some number 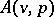 , and assume that this set is not empty. This set of a priori distributions on the parameter space is an example of a conjugate family. This means that if the random variable
, and assume that this set is not empty. This set of a priori distributions on the parameter space is an example of a conjugate family. This means that if the random variable 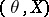 has distribution
has distribution 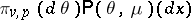 , then the distribution of
, then the distribution of 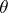 conditioned by
conditioned by 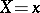 (a posteriori distribution) is
(a posteriori distribution) is 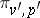 for some
for some 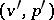 depending on
depending on 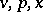 . See [a1] for a complete study; however, [a3] is devoted to the case
. See [a1] for a complete study; however, [a3] is devoted to the case 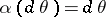 , which has special properties and has, for many years, been the only serious study of the subject.
, which has special properties and has, for many years, been the only serious study of the subject.
References
| [a1] | S. Bar-Lev, P. Enis, G. Letac, "Sampling models which admit a given general exponential family as a conjugate family of priors" Ann. Statist. , 22 (1994) pp. 1555–1586 |
| [a2] | O. Barndorff-Nielsen, "Information and exponential families in statistical theory" , Wiley (1978) |
| [a3] | P. Diaconis, D. Ylvizaker, "Conjugate priors for exponential families" Ann. Statist. , 7 (1979) pp. 269–281 |
| [a4] | B. Jorgensen, "Exponential dispersion models" J. R. Statist. Soc. Ser. B , 49 (1987) pp. 127–162 |
| [a5] | G. Letac, "Lectures on natural exponential families and their variance functions" , Monogr. Mat. , 50 , Inst. Mat. Pura Aplic. Rio (1992) |
Exponential family of probability distributions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Exponential_family_of_probability_distributions&oldid=17972