Exceptional value
A concept in value-distribution theory. Let 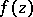 be a meromorphic function in the whole
be a meromorphic function in the whole  -plane and let
-plane and let 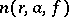 denote its number of
denote its number of  -points (counting multiplicities) in the disc
-points (counting multiplicities) in the disc 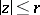 . According to R. Nevanlinna's first fundamental theorem (cf. [1]), as
. According to R. Nevanlinna's first fundamental theorem (cf. [1]), as 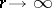 ,
,
 |
where 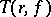 is the characteristic function, which does not depend on
is the characteristic function, which does not depend on  ,
, 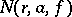 is the counting function (the logarithmic average of
is the counting function (the logarithmic average of 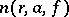 ) and
) and  is a function expressing the average proximity of the values of
is a function expressing the average proximity of the values of 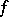 to
to  on
on  (cf. Value-distribution theory). For the majority of values
(cf. Value-distribution theory). For the majority of values  the quantities
the quantities 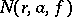 and
and 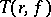 are asymptotically equivalent, as
are asymptotically equivalent, as 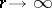 . A (finite or infinite) number
. A (finite or infinite) number  is called an exceptional value if this equivalence as
is called an exceptional value if this equivalence as 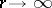 is violated. One distinguishes several kinds of exceptional values.
is violated. One distinguishes several kinds of exceptional values.
A number  is called an exceptional value of
is called an exceptional value of 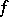 in the sense of Poincaré if the number of
in the sense of Poincaré if the number of  -points of
-points of 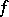 in the whole plane is finite (cf. [1], [2]), in particular if
in the whole plane is finite (cf. [1], [2]), in particular if 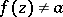 for any
for any  .
.
A number  is called an exceptional value of
is called an exceptional value of 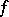 in the sense of Borel if
in the sense of Borel if 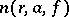 grows slower, in a certain sense, than
grows slower, in a certain sense, than 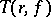 , as
, as 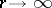 (cf. [1], [2]).
(cf. [1], [2]).
A number  is called an exceptional value of
is called an exceptional value of 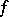 in the sense of Nevanlinna (cf. [1]) if its defect (cf. Defective value)
in the sense of Nevanlinna (cf. [1]) if its defect (cf. Defective value)
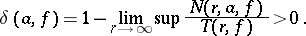 |
A number  is called an exceptional value of
is called an exceptional value of 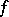 in the sense of Valiron if
in the sense of Valiron if
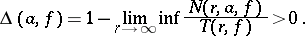 |
A number  for which
for which
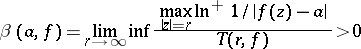 |
is also called an exceptional value for 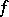 . The quantity
. The quantity 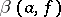 (the positive deviation of
(the positive deviation of 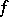 ) characterizes the rate of the asymptotic approximation of
) characterizes the rate of the asymptotic approximation of 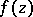 to
to  (cf. [3]).
(cf. [3]).
References
| [1] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [2] | A.A. Gol'dberg, I.V. Ostrovskii, "Value distribution of meromorphic functions" , Moscow (1970) (In Russian) |
| [3] | V.P. Petrenko, "Growth of meromorphic functions of finite lower order" Math. USSR Izv. , 3 : 2 (1969) pp. 391–432 Izv. Akad. Nauk SSSR Ser. Mat. , 33 : 2 (1969) pp. 414–454 |
Comments
An  -point of
-point of 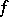 is a point
is a point  such that
such that 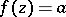 .
.
Exceptional value. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Exceptional_value&oldid=18994