Excellent ring
A commutative Noetherian ring satisfying the three axioms stated below. It is known that a geometric ring possesses several qualitative properties not inherent in arbitrary Noetherian rings. The concept of an excellent ring makes it possible to take the most important properties of geometric rings axiomatically into account.
Axioms of an excellent ring  .
.
A1. The ring  is a universal chain ring. (A ring
is a universal chain ring. (A ring  is said to be a chain ring if for any two prime ideals
is said to be a chain ring if for any two prime ideals  of it the lengths of any two saturated chains
of it the lengths of any two saturated chains  of prime ideals are the same. A ring
of prime ideals are the same. A ring  is said to be a universal chain ring if any polynomial ring
is said to be a universal chain ring if any polynomial ring  is a chain ring.)
is a chain ring.)
A2. The formal fibres of 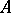 are geometrically regular, i.e. for any prime ideal
are geometrically regular, i.e. for any prime ideal  and any homomorphism from
and any homomorphism from 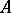 into a field
into a field 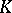 , the ring
, the ring  is regular. Here
is regular. Here 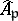 is the completion of the local ring
is the completion of the local ring 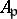 .
.
A3. For any integral finite 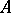 -algebra
-algebra 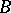 there is a non-zero element
there is a non-zero element 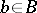 such that the ring of fractions,
such that the ring of fractions, 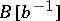 , is regular.
, is regular.
Excellent rings possess the following properties:
1) For an excellent ring 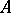 , the set of regular (normal) points of the scheme
, the set of regular (normal) points of the scheme 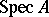 is open.
is open.
2) If an excellent local ring  is reduced (normal or equi-dimensional), then so is the completion
is reduced (normal or equi-dimensional), then so is the completion 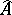 .
.
3) The integral closure of an excellent ring 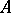 in a finite extension of the field of fractions of
in a finite extension of the field of fractions of 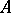 is a finite
is a finite 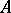 -algebra.
-algebra.
4) If a ring 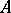 is excellent, then any
is excellent, then any 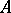 -algebra of finite type is also an excellent ring.
-algebra of finite type is also an excellent ring.
Two important examples of excellent rings are the complete local rings (or analytic rings) and the Dedekind rings with field of fractions of characteristic zero. Therefore, the class of excellent rings is sufficiently large and contains, in particular, all algebras of finite type over a field or over the ring 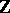 of integers.
of integers.
The excellency of a ring 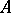 is closely connected with the possibility of resolution of singularities of the scheme
is closely connected with the possibility of resolution of singularities of the scheme 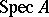 (cf. [1] and [2]).
(cf. [1] and [2]).
References
| [1] | A. Grothendieck, J. Dieudonne, "Eléments de géométrie algébrique" Publ. Math. IHES , 2 (1965) |
| [2] | H. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero. I" Ann. of Math. , 79 : 1 (1964) pp. 109–203 |
Comments
A chain ring is also called a catenarian ring. A sequence of prime ideals 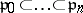 is saturated if there is no prime ideal
is saturated if there is no prime ideal 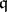 and integer
and integer 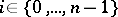 such that
such that 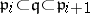 , with both inclusions strict. An excellent ring is a universal Japanese ring. An integer domain
, with both inclusions strict. An excellent ring is a universal Japanese ring. An integer domain 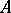 is
is 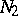 if for every finite extension
if for every finite extension 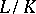 of its field fractions
of its field fractions 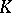 the integral closure
the integral closure 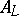 of
of 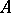 in
in 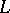 is a finite
is a finite  -module. A ring
-module. A ring 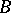 is universal Japanese if it is Noetherian and if
is universal Japanese if it is Noetherian and if 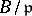 is
is 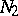 for every prime ideal
for every prime ideal 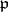 of
of  . Other terminology for universal Japanese: Nagata ring, pseudo-geometric ring. Cf. also Geometric ring.
. Other terminology for universal Japanese: Nagata ring, pseudo-geometric ring. Cf. also Geometric ring.
Excellent ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Excellent_ring&oldid=17044