Evolvent of a plane curve
2020 Mathematics Subject Classification: Primary: 53A04 [MSN][ZBL]
involute
A curve $\bar\gamma$ assigned to the plane curve $\gamma$ such that $\gamma$ is the evolute of $\bar\gamma$. If $\mathbf{r} = \mathbf{r}(s)$ (where $s$ is the arc length parameter of $\gamma$) is the equation of $\gamma$, then the equation of its evolvent has the form $$ \bar{\mathbf{r}} = \mathbf{r}(s) + (c-s)\tau(s) \,, $$ where $c$ is an arbitrary constant and $\tau$ the unit tangent vector to $\gamma$. The figures show the construction of the evolvent in two typical cases: a) if for any $s<c$ the curvature $k(s)$ of $\gamma$ does not vanish (the evolvent is a regular curve); and b) if $k(s)$ vanishes only for $s=s_1$ and $k'(s_1) \ne 0$ (the point corresponding to $s=s_1$ on the evolvent is a cusp of the second kind).
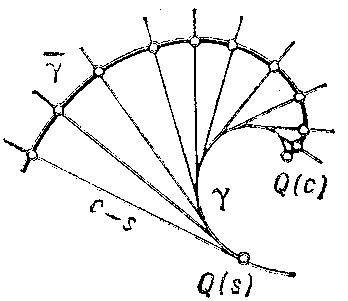
Figure: e036720a
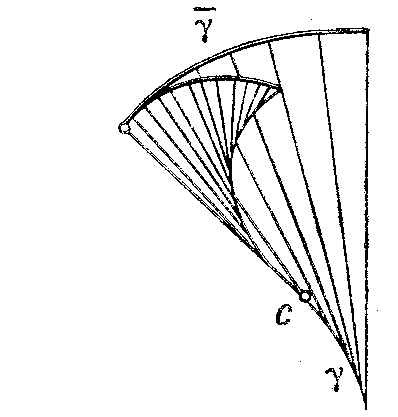
Figure: e036720b
About the evolvent of a surface, see Evolute (surface).
Comments
The evolvent is often called the involute of the curve. Involvents play a part in the construction of gears.
For references see also Evolute.
References
| [a1] | K. Strubecker, "Differential geometry" , I , de Gruyter (1964) |
| [a2] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) pp. 305ff (Translated from French) |
| [a3] | J.L. Coolidge, "A treatise on algebraic plane curves" , Dover, reprint (1959) pp. 195 |
| [a4] | H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) pp. 25; 60 |
| [a5] | M. Berger, "Geometry" , I , Springer (1987) pp. 253–254 |
Evolvent of a plane curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Evolvent_of_a_plane_curve&oldid=42553