Euler transformation

The Euler transformation of series. Given a series

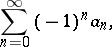(1)

the series

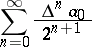(2)

is said to be obtained from (1) by means of the Euler transformation. Here

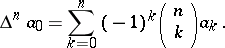If the series (1) converges, then so does (2), and to the same sum as (1). If the series (2) converges (in this case (1) may diverge), then the series (1) is called Euler summable.

If (1) converges, if 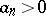, if the sequences

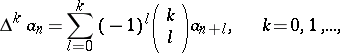are monotone, and if

then the series (2) converges more rapidly than (1) (see Convergence, types of).

L.D. Kudryavtsev

Euler's transformation is the integral transformation

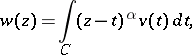(1)

where 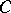is a contour in the complex 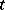-plane. It was proposed by L. Euler (1769).

The Euler transformation is applied to linear ordinary differential equations of the form

(2)

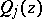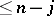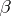where is a polynomial of degree and is a constant. Any linear equation of the form

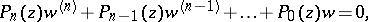where the 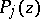are polynomials of degree 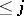and the degree of 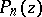is , can be written in the form (2). The equation

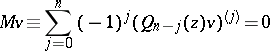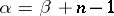is called the Euler transform of (2). If is defined by (1) and , then

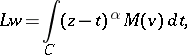provided that the integrated term arising from integration by parts vanishes. From this it follows that if 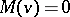, then 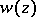is a solution of (2).

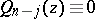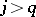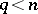The Euler transformation makes it possible to reduce the order of (2) if for , . For 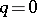and 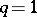equation (2) can be integrated (see Pochhammer equation).

References

[1]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956)
[2]	E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Teubner (1943)

M.V. Fedoryuk

The Euler transform of the first kind is the integral transform

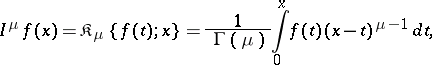where and are complex variables and the path of integration is the segment , .

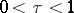The Euler transform of the first kind is also called the fractional Riemann–Liouville integral of order 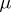. (Sometimes the name of Riemann–Liouville integral is given to

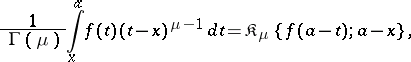where is a complex number.)

If 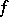and 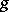satisfy certain conditions, then

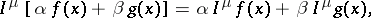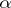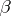where and are complex constants and

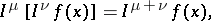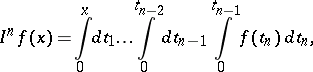The Euler transform of the second kind is the integral transform

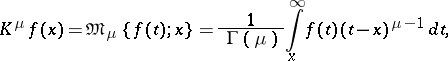where 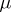and are complex variables and the path of integration is the ray 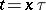, , 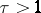or 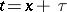, 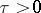. Under certain conditions,

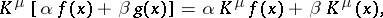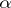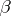where and are complex constants and

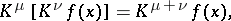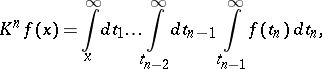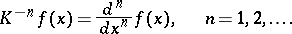The Euler transform of the second kind is sometimes called the fractional Weyl integral of order .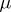

The above transforms have also been introduced for generalized functions.

References

[1]	Y.A. Brychkov, A.P. Prudnikov, "Integral transformations of generalized functions" , Gordon & Breach (1988) (Translated from Russian)

Yu.A. BrychkovA.P. Prudnikov

Comments

See also Fractional integration and differentiation.

References

[a1]	A. Erdélyi, W. Magnus, F. Oberhetinger, F.G. Tricomi, "Tables of integral transforms" , II , McGraw-Hill (1954) pp. Chapt. 13
[a2]	A.C. McBride, "Fractional calculus and integral transforms of generalized functions" , Pitman (1979)