Euler summation method

One of the methods for summing series of numbers and functions. A series

(*)

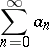is summable by means of the Euler summation method (-summable) to the sum if

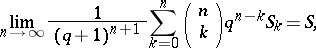where and .

The method was first applied by L. Euler for to sum slowly-convergent or divergent series. Since the technique was later extended to arbitrary values of by K. Knopp [1], it is also known for arbitrary as the Euler–Knopp summation method. This method is regular for 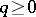(see Regular summation methods); if a series is 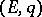-summable, then it is also 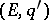-summable, , to the same sum (see Inclusion of summation methods). For 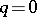the summability of the series (*) by the Euler summation method implies that the series is convergent. If the series is -summable, then its terms 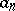satisfy the condition 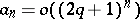, 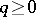. The Euler summation method can also be applied for analytic continuation beyond the disc of convergence of a function defined by means of a power series. Thus, the series is 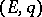-summable to the sum 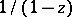in the disc with centre at 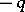and of radius .

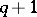References

[1]	K. Knopp, "Ueber das Eulersche Summierungsverfahren" Math. Z. , 15 (1922) pp. 226–253
[2]	K. Knopp, "Ueber das Eulersche Summierungsverfahren II" Math. Z. , 18 (1923) pp. 125–156
[3]	G.H. Hardy, "Divergent series" , Clarendon Press (1949)
[4]	S. Baron, "Introduction to theory of summation of series" , Tallin (1977) (In Russian)

References

[a1]	K. Zeller, W. Beekmann, "Theorie der Limitierungsverfahren" , Springer (1970)