Euler function
From Encyclopedia of Mathematics
The arithmetic function 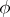 whose value at
whose value at  is equal to the number of positive integers not exceeding
is equal to the number of positive integers not exceeding  and relatively prime to
and relatively prime to  . The Euler function is multiplicative, that is
. The Euler function is multiplicative, that is 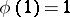 and
and 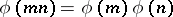 for
for 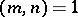 . The function
. The function 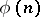 satisfies the relations
satisfies the relations
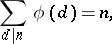 |
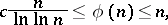 |
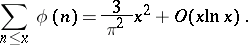 |
It was introduced by L. Euler (1763).
References
| [1] | K. Chandrasekharan, "Introduction to analytic number theory" , Springer (1968) |
Comments
The function 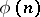 can be evaluated by
can be evaluated by 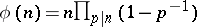 , where the product is taken over all primes dividing
, where the product is taken over all primes dividing  , cf. [a1].
, cf. [a1].
For a derivation of the asymptotic formula in the article above, as well as of the formula
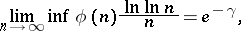 |
where 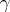 is the Euler constant, see also [a1], Chapts. 18.4 and 18.5.
is the Euler constant, see also [a1], Chapts. 18.4 and 18.5.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapts. 5; 7; 8 |
How to Cite This Entry:
Euler function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_function&oldid=11814
Euler function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_function&oldid=11814
This article was adapted from an original article by S.A. Stepanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article