Euler angles
The angles  ,
,  and
and  that determine the position of one Cartesian rectangular coordinate system
that determine the position of one Cartesian rectangular coordinate system  relative to another one
relative to another one  with the same origin and orientation. The Euler angles are regarded as the angles through which the former must be successively rotated about the axes of the latter so that in the end the two systems coincide (see Fig.).
with the same origin and orientation. The Euler angles are regarded as the angles through which the former must be successively rotated about the axes of the latter so that in the end the two systems coincide (see Fig.).

Figure: e036390a
Let  be the axis coinciding with the line of intersection of the planes
be the axis coinciding with the line of intersection of the planes  and
and  , oriented so that the three lines
, oriented so that the three lines  ,
, 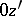 and
and  form a right-handed triple. Then
form a right-handed triple. Then 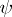 is the angle between
is the angle between 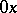 and
and  , measured in the plane
, measured in the plane 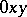 from
from 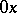 in the direction of the shortest rotation of
in the direction of the shortest rotation of 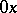 to
to 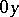 ,
, 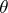 is the angle between
is the angle between 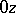 and
and 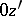 not exceeding
not exceeding  , and
, and 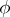 is in the direction of the shortest rotation of
is in the direction of the shortest rotation of 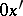 to
to 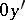 . The coordinates
. The coordinates 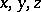 , and
, and 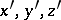 are connected by the relations
are connected by the relations
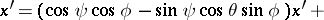 |
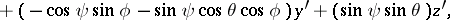 |
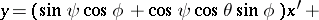 |
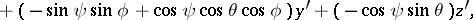 |
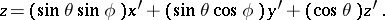 |
These angles were introduced by L. Euler (1748).
Comments
For other formulas, as well as applications, see [a1]–[a3].
References
| [a1] | L.D. Landau, E.M. Lifshits, "Mechanics" , Pergamon (1965) (Translated from Russian) |
| [a2] | G. Gallavotti, "The elements of mechanics" , Springer (1983) |
| [a3] | H. Goldstein, "Classical mechanics" , Addison-Wesley (1959) |
Euler angles. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_angles&oldid=15870