Euler-Poisson-Darboux equation
The second-order hyperbolic partial differential equation
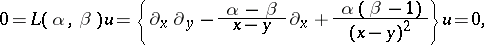 |
where  and
and  are real positive parameters such that
are real positive parameters such that  (see [a8]) and
(see [a8]) and  denotes the partial derivative of the function
denotes the partial derivative of the function  with respect to
with respect to  .
.
This equation appears in various areas of mathematics and physics, such as the theory of surfaces [a4], the propagation of sound [a3], the colliding of gravitational waves [a6], etc.. The Euler–Poisson–Darboux equation has rather interesting properties, e.g. in relation to Miller symmetry and the Laplace sequence, and has a relation to, e.g., the Toda molecule equation (see [a4]).
A formal solution to the Euler–Poisson–Darboux equation has the form [a8]
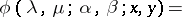 |
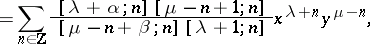 |
where 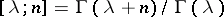 and
and 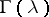 is the gamma-function.
is the gamma-function.
By conjugate transformation of the differential operator 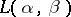 with
with 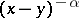 one obtains the operator
one obtains the operator
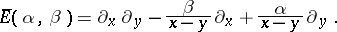 | (a1) |
Many papers deal with the equation
 | (a2) |
(see, e.g., [a11], [a8], [a7], [a10], [a12]). In the characteristic triangle  and under the conditions
and under the conditions
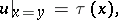 | (a3) |
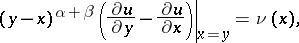 |
the solution of (a2) can be expressed as (see [a12]):
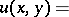 |
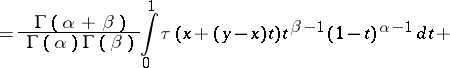 |
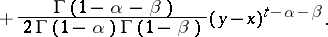 |
 |
Formulas for the general solution of (a2) are known for  ,
,  ;
;  ; and
; and 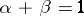 . For other values of the parameters, an explicit representation of the solution can be given using a regularization method for the divergent integral (see [a7]). The unique solvability of a boundary value problem for (a2) with a non-local boundary condition, containing the Szegö fractional integration and differentiation (cf. Fractional integration and differentiation) operators, is proved in [a11]. For (a2) local solutions, propagation of singularities, and holonomic solutions of hypergeometric type are studied in [a14]. For hypergeometric functions of several variables occurring as solutions of boundary value problems for (a2), see also [a14].
. For other values of the parameters, an explicit representation of the solution can be given using a regularization method for the divergent integral (see [a7]). The unique solvability of a boundary value problem for (a2) with a non-local boundary condition, containing the Szegö fractional integration and differentiation (cf. Fractional integration and differentiation) operators, is proved in [a11]. For (a2) local solutions, propagation of singularities, and holonomic solutions of hypergeometric type are studied in [a14]. For hypergeometric functions of several variables occurring as solutions of boundary value problems for (a2), see also [a14].
A  -difference analogue of the operator
-difference analogue of the operator 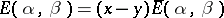 is considered in [a8]; it has been proved that the
is considered in [a8]; it has been proved that the 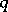 -deformation of
-deformation of 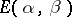 is the
is the  -difference operator
-difference operator 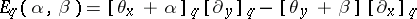 .
.
The existence and uniqueness of global generalized solutions of mixed problems for the generalized Euler–Poisson–Darboux equation
 | (a4) |
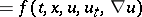 |
are studied in [a15], using Galerkin approximation. Moreover, the classical solution of (a4) has been obtained by using properties of Sobolev spaces and imbedding theorems (cf. also Imbedding theorems). See [a2], [a11], [a1], [a9] for various aspects of (a4).
See [a5] for necessary and sufficient conditions for stabilization of the solution of the Cauchy problem for the Euler–Poisson–Darboux equation in a homogeneous symmetric space.
References
| [a1] | C.Y. Chan, K.K. Nip, "Quenching for semilinear Euler–Poisson–Darboux equations" J. Wiener (ed.) , Partial Differential Equations. Proc. Internat. Conf. Theory Appl. Differential Equations (Univ. Texas-Pan American, Edinburg, Texas, May 15-18, 1991) , Pitman Res. Notes , 273 , Longman (1992) pp. 39–43 |
| [a2] | C.Y. Chan, K.K. Nip, "On the blow-up of 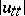 at quenching for semilinear Euler–Poisson–Darboux equations" Comput. Appl. Math. , 14 : 2 (1995) pp. 185–190 at quenching for semilinear Euler–Poisson–Darboux equations" Comput. Appl. Math. , 14 : 2 (1995) pp. 185–190 |
| [a3] | E.T. Copson, "Partial differential equations" , Cambridge Univ. Press (1975) |
| [a4] | G. Darboux, "Sur la théeorie générale de surfaces" , II , Chelsea, reprint (1972) |
| [a5] | V.N. Denisov, "On the stabilization of means of the solution of the Cauchy problem for hyperbolic equations in symmetric spaces" Soviet Math. Dokl. , 42 : 3 (1991) pp. 738–742 Dokl. Akad. Nauk. SSSR , 315 : 2 (1990) pp. 266–271 |
| [a6] | I. Hauser, F.J. Ernst, "Initial value problem for colliding gravitational plane wave" J. Math. Phys. , 30 : 4 (1989) pp. 872–887 |
| [a7] | R.S. Khairullin, "On the theory of the Euler–Poisson–Darboux equation" Russian Math. , 37 : 11 (1993) pp. 67–74 Izv. Vyssh. Uchebn. Zaved. Mat. : 11 (1993) pp. 69–76 |
| [a8] | K. Nagamoto, Y. Koga, "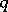 -difference analogue of the Euler–Poisson–Darboux equation and its Laplace sequence" Osaka J. Math. , 32 : 2 (1995) pp. 451–465 -difference analogue of the Euler–Poisson–Darboux equation and its Laplace sequence" Osaka J. Math. , 32 : 2 (1995) pp. 451–465 |
| [a9] | S.V. Pan'ko, "On a representation of the solution of a generalized Euler–Poisson–Darboux equation" Diff. Uravnen. , 28 : 2 (1992) pp. 278–281 (In Russian) |
| [a10] | O.A. Repin, "Boundary value problems with shift for equations of hyperbolic and mixed type" , Samara: Izd. Sartovsk. Univ. (1992) (In Russian) |
| [a11] | O.A. Repin, "A nonlocal boundary value problem for the Euler–Poisson–Darboux equation" Diff. Eqs. , 31 : 1 (1995) pp. 160–162 Diff. Uravn. , 31 : 1 (1995) pp. 171–172 |
| [a12] | M. Saigo, "A certain boundary value problem for the Euler–Poisson–Darboux equation" Math. Japon. , 24 : 4 (1979) pp. 377–385 |
| [a13] | M.M. Smirnov, "Degenerate hyperbolic equations" , Izd. Vysh. Shkola, Minsk (1977) (In Russian) |
| [a14] | N. Takayama, "Propagation of singularities of solutions of the Euler–Poisson–Darboux equation and a global structure of the space of holonomic solutions I" Funkc. Ekvacioj, Ser. Internat. , 35 (1992) pp. 343–403 |
| [a15] | J. Wang, "Mixed problems for nonlinear hyperbolic equations with singular dissipative terms" Acta Math. Appl. Sin. , 16 (1993) pp. 23–30 (In Chinese) (English summary) |
Euler-Poisson-Darboux equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler-Poisson-Darboux_equation&oldid=12800