Euler-Frobenius polynomials
The Euler–Frobenius polynomials  of degree
of degree  are characterized by the Frobenius reciprocal identity ([a1], [a2], [a3])
are characterized by the Frobenius reciprocal identity ([a1], [a2], [a3])
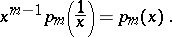 |
Thus,  is invariant under the reflection
is invariant under the reflection
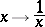 |
of the indeterminate  . The best way to implement an invariance of this kind is to look for an appropriate space with which the Euler–Frobenius polynomials
. The best way to implement an invariance of this kind is to look for an appropriate space with which the Euler–Frobenius polynomials 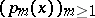 are attached in a spectral geometric way.
are attached in a spectral geometric way.
So, let  denote a symplectic vector space of dimension
denote a symplectic vector space of dimension  (cf. also Symplectic space). Then the characteristic polynomial of each symplectic automorphism of
(cf. also Symplectic space). Then the characteristic polynomial of each symplectic automorphism of  is an Euler–Frobenius polynomial
is an Euler–Frobenius polynomial 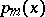 of odd degree
of odd degree 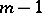 .
.
The proof follows from the fact that the determinant of each symplectic automorphism  of
of 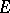 equals
equals  , so that there is a natural imbedding
, so that there is a natural imbedding
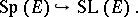 |
Thus, 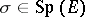 preserves the symplectic volume spanned by
preserves the symplectic volume spanned by 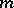 vectors of the vector space
vectors of the vector space 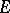 .
.
A consequence is that each eigenvalue 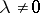 of a symplectic endomorphism
of a symplectic endomorphism 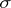 of
of  having multiplicity
having multiplicity  gives rise to a reciprocal eigenvalue
gives rise to a reciprocal eigenvalue 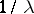 of the same multiplicity
of the same multiplicity 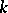 .
.
In view of the self-reciprocal eigenvalue
 |
of 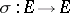 for even
for even  , of course, spectral theory suggests a complex contour integral representation of the Euler–Frobenius polynomials
, of course, spectral theory suggests a complex contour integral representation of the Euler–Frobenius polynomials 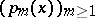 , as follows.
, as follows.
Let 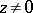 denote a complex number such that
denote a complex number such that 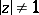 . Let
. Let 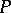 denote a path in the complex plane
denote a path in the complex plane 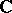 which forms the boundary of a closed vertical strip in the open right or left half-plane of
which forms the boundary of a closed vertical strip in the open right or left half-plane of 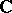 according as
according as 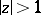 or
or 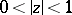 , respectively. Let
, respectively. Let 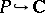 be oriented so that its topological index satisfies
be oriented so that its topological index satisfies 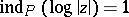 . Then, for each integer
. Then, for each integer 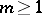 , the complex contour integral representation
, the complex contour integral representation
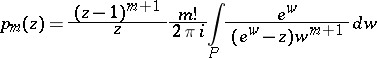 |
holds.
The proof follows from the expansion
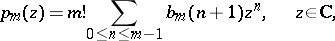 |
with strictly positive integer coefficients, where 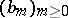 denote the basis spline functions (cf. [a3] and also Spline).
denote the basis spline functions (cf. [a3] and also Spline).
A consequence is that the Euler–Frobenius polynomials provide the coefficients of the local power series expansion of the function
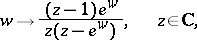 |
which is meromorphic on the complex plane 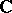 .
.
The Euler–Frobenius polynomials 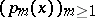 satisfy the three-term recurrence relation
satisfy the three-term recurrence relation
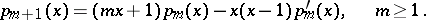 |
A direct proof follows from the complex contour integral representations of the derivatives  , which can be derived from the complex contour integral representation given above for the Euler–Frobenius polynomials.
, which can be derived from the complex contour integral representation given above for the Euler–Frobenius polynomials.
The preceding recurrence relation opens a simple way to calculate the coefficients of the Euler–Frobenius polynomials 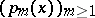 ([a1], [a3]).
([a1], [a3]).
References
| [a1] | L. Euler, "Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum" , Acad. Imper. Sci. Petropolitanæ (1775) (Opera Omnis Ser. I (Opera Math.), Vol. X, Teubner, 1913) |
| [a2] | F.G. Frobenius, "Über die Bernoullischen Zahlen und die Eulerschen Polynome" Sitzungsber. K. Preuss. Akad. Wissenschaft. Berlin (1910) pp. 809–847 (Gesammelte Abh. Vol. III, pp. 440-478, Springer 1968) |
| [a3] | W. Schempp, "Complex contour integral representation of cardinal spline functions" , Contemp. Math. , 7 , Amer. Math. Soc. (1982) |
Euler-Frobenius polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler-Frobenius_polynomials&oldid=17228