Euclidean ring
From Encyclopedia of Mathematics
An integral domain with an identity such that to each non-zero element  of it corresponds a non-negative integer
of it corresponds a non-negative integer  satisfying the following requirement: For any two elements
satisfying the following requirement: For any two elements  and
and  with
with 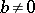 one can find elements
one can find elements  and
and  such that
such that
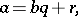 |
where either 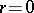 or
or 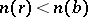 .
.
Every Euclidean ring is a principal ideal ring and hence a factorial ring; however, there exist principal ideal rings that are not Euclidean. Euclidean rings include the ring of integers (the absolute value 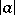 plays the part of
plays the part of 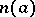 ), and also the ring of polynomials in one variable over a field (
), and also the ring of polynomials in one variable over a field (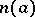 is the degree of the polynomial). In any Euclidean ring the Euclidean algorithm can be used to find the greatest common divisor of two elements.
is the degree of the polynomial). In any Euclidean ring the Euclidean algorithm can be used to find the greatest common divisor of two elements.
References
| [1] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
How to Cite This Entry:
Euclidean ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euclidean_ring&oldid=18798
Euclidean ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euclidean_ring&oldid=18798
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article