Euclidean algorithm

A method for finding the greatest common divisor of two integers, two polynomials (and, in general, two elements of a Euclidean ring) or the common measure of two intervals. It was described in geometrical form in Euclid's Elements (3rd century B.C.).

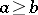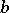For two positive integers , the method is as follows. Division with remainder of by always leads to the result 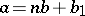, where the quotient is a positive integer and the remainder 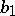is either 0 or a positive integer less than 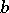, 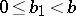. Successive divisions are performed:

(*)

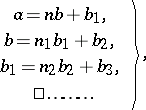where the 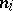are positive integers and 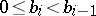, until a remainder 0 is obtained. The series of equations (*) finishes thus:

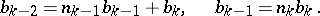The least positive remainder 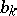in this process is the greatest common divisor of and .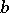

The Euclidean algorithms for polynomials or for intervals are similar to the one for integers. In the case of incommensurable intervals the Euclidean algorithm leads to an infinite process.

Comments

The Euclidean algorithm to determine the greatest common divisor of two integers 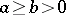is quite fast. It can be shown that the number of steps required is at most

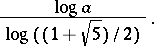A slight extension of the algorithm also yields a solution of 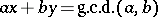in .

References

[a1]	W.J. Leveque, "Topics in number theory" , 1 , Addison-Wesley (1956) pp. Chapt. 2