Eta-invariant
 -invariant
-invariant
Let  be an unbounded self-adjoint operator with only pure point spectrum (cf. also Spectrum of an operator). Let
be an unbounded self-adjoint operator with only pure point spectrum (cf. also Spectrum of an operator). Let  be the eigenvalues of
be the eigenvalues of  , counted with multiplicity. If
, counted with multiplicity. If  is a first-order elliptic differential operator on a compact manifold, then
is a first-order elliptic differential operator on a compact manifold, then  and the series
and the series
 |
is convergent for  large enough. Moreover,
large enough. Moreover, 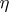 has a meromorphic continuation to the complex plane, with
has a meromorphic continuation to the complex plane, with  a regular value (cf. also Analytic continuation). The value of
a regular value (cf. also Analytic continuation). The value of  at
at  is called the eta-invariant of
is called the eta-invariant of 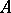 , and was introduced by M.F. Atiyah, V.K. Patodi and I.M. Singer in the foundational paper [a1] as a correction term for an index theorem on manifolds with boundary (cf. also Index formulas). For example, in that paper, they prove that the signature
, and was introduced by M.F. Atiyah, V.K. Patodi and I.M. Singer in the foundational paper [a1] as a correction term for an index theorem on manifolds with boundary (cf. also Index formulas). For example, in that paper, they prove that the signature 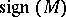 of a compact, oriented,
of a compact, oriented, 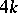 -dimensional Riemannian manifold with boundary
-dimensional Riemannian manifold with boundary 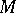 whose metric is a product metric near the boundary is
whose metric is a product metric near the boundary is
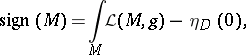 |
where 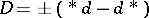 is the signature operator on the boundary and
is the signature operator on the boundary and  the Hirzebruch
the Hirzebruch 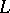 -polynomial associated to the Riemannian metric on
-polynomial associated to the Riemannian metric on  .
.
The definition of the eta-invariant was generalized by J.-M. Bismut and J. Cheeger in [a2], where they introduced the eta-form of a family of elliptic operators as above. It can be used to recover the eta-invariant of operators in the family.
References
| [a1] | M.F. Atiyah, V.K. Patodi, I.M. Singer, "Spectral asymmetry and Riemannian Geometry" Math. Proc. Cambridge Philos. Soc. , 77 (1975) pp. 43–69 |
| [a2] | J.-M. Bismut, J. Cheeger, "Eta invariants and their adiabatic limits" J. Amer. Math. Soc. , 2 : 1 (1989) pp. 33–77 |
Eta-invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Eta-invariant&oldid=17359