Essentially-undecidable theory
An algorithmically-undecidable logical theory, all consistent extensions of which are also undecidable (see Undecidability). An elementary theory is an essentially-undecidable theory if and only if every model of it has an undecidable elementary theory. Every complete undecidable theory is an essentially-undecidable theory, as is formal arithmetic (cf. Arithmetic, formal); no theory with a finite model can be an essentially-undecidable theory.
The essential undecidability of a suitable finitely-axiomatizable elementary theory  is often used in proving the undecidability of a given theory
is often used in proving the undecidability of a given theory 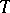 (see [1], [2]). In this proof,
(see [1], [2]). In this proof,  is interpreted in any model
is interpreted in any model  of
of  . The domain of interpretation and the values of the elements of the signature of
. The domain of interpretation and the values of the elements of the signature of  are defined using values in the model
are defined using values in the model  of suitable formulas in the language of
of suitable formulas in the language of  . If the interpretation is a model of
. If the interpretation is a model of  , then
, then 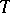 is undecidable; moreover, this theory is hereditarily undecidable, i.e. all of its subtheories of the same signature as
is undecidable; moreover, this theory is hereditarily undecidable, i.e. all of its subtheories of the same signature as 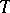 are undecidable. This method is used to prove the undecidability of elementary predicate logic, elementary group theory, elementary field theory, etc. Finitely-axiomatized formal arithmetic is often used as the essentially-undecidable theory
are undecidable. This method is used to prove the undecidability of elementary predicate logic, elementary group theory, elementary field theory, etc. Finitely-axiomatized formal arithmetic is often used as the essentially-undecidable theory 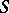 .
.
References
| [1] | A. Tarski, A. Mostowski, R.M. Robinson, "Undecidable theories" , North-Holland (1953) |
| [2] | Yu.L. Ershov, I.A. Lavrov, A.D. Taimanov, M.A. Taitslin, "Elementary theories" Russian Math. Surveys , 20 : 4 (1965) pp. 35–105 Uspekhi Mat. Nauk , 20 : 4 (1965) pp. 37–108 |
| [3] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
Essentially-undecidable theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Essentially-undecidable_theory&oldid=17241