Erlangen program
A unified way of looking at various geometries (for example, Euclidean, affine, projective). It was first pronounced by F. Klein in his inaugural lecture in 1872 at the University of Erlangen (Germany) and was printed later with the title Vergleichende Betrachtungen über neuere geometrische Forschungen [1].
The essence of the Erlangen program consists in the following. As is well known, Euclidean geometry considers the properties of figures that do not change under rigid motions; equal figures are defined as those that can be transferred onto one another by a motion. But instead of motions one may choose any other collection of geometric transformations and declare as "equal" those figures that are obtained from one another by transformations of this collection. This leads to another "geometry" , which studies the properties of figures that do not change under such transformations. The relevant "equality" must satisfy the following three natural conditions: 1) every figure 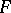 is "equal" to itself; 2) if a figure
is "equal" to itself; 2) if a figure 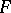 is "equal" to
is "equal" to 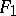 , then
, then 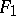 is "equal" to
is "equal" to 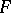 ; and 3) if
; and 3) if 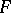 is "equal" to
is "equal" to 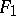 and
and 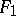 to
to 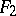 , then
, then 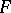 is "equal" to
is "equal" to 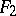 . Accordingly, one has to require that the collection of transformations in question is a group. The theory that studies the properties of figures that are preserved under all transformations of a given group is called the geometry of this group.
. Accordingly, one has to require that the collection of transformations in question is a group. The theory that studies the properties of figures that are preserved under all transformations of a given group is called the geometry of this group.
The choice of distinct transformation groups leads to distinct geometries. Thus, the analysis of the group of motions leads to the usual (Euclidean) geometry; when motions are replaced by affine or projective transformations, the result is affine or projective geometry. On the basis of ideas of A. Cayley, Klein proved that if one starts out from projective transformations that carry a certain circle (or any other conic) into itself, one comes to the non-Euclidean Lobachevskii geometry. Klein introduced into the discussion a fairly broad range of other geometries defined in a similar fashion.
The Erlangen program does not comprise some important branches of geometry such as Riemannian geometry. However, it had a substantial stimulating value for the subsequent development of geometry.
References
| [1] | F. Klein, "Vergleichende Betrachtungen über neuere geometrische Forschungen" Math. Ann. , 43 (1893) pp. 63–100 ((Also: Gesammelte Abh. Vol. 1, Springer, 1921, pp. 460–497)) |
| [2] | F. Klein, "Elementary mathematics from advanced standpoint" , Dover, reprint (1945) (Translated from German) |
| [3] | F. Klein, "Vorlesungen über höhere Geometrie" , Springer (1926) |
| [4] | N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) |
Comments
References
| [a1] | M. Greenberg, "Euclidean and Non-Euclidean geometry" , Freeman (1980) |
Erlangen program. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Erlangen_program&oldid=14802