Erlang distribution

The probability distribution concentrated on 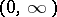with density

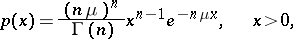where the integer and the real number are parameters. The characteristic function of the Erlang distribution has the form

and the mathematical expectation and variance are 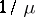and 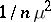, respectively.

The Erlang distribution is special case of the gamma-distribution: 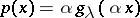, where 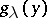is the density of the gamma-distribution for 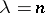, and where 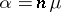. For 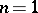the Erlang distribution is the same as the exponential distribution with parameter 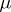. The Erlang distribution with parameters and 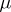can be found as the distribution of the sum of independent random variables having the same exponential distribution with parameter 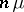. As 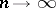, the Erlang distribution tends to the degenerate distribution concentrated at the point .

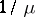The selection of the Erlang distribution from the system of gamma-distributions is explained by its use in queueing theory. In many random queueing processes the Erlang distribution appears as the distribution of intervals among random events or as the distribution of the queueing time. Sometimes the Erlang distribution is defined as the gamma-distribution with the density

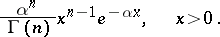It is named for A. Erlang, who was the first to construct mathematical models in queueing problems.

References

[1]	T.L. Saaty, "On elements of queueing theory with applications" , McGraw-Hill (1961)