Ergodic set
in the phase space 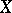 (a metrizable compactum) of a topological dynamical system
(a metrizable compactum) of a topological dynamical system 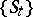 (a flow (continuous-time dynamical system) or a cascade) corresponding to a normalized ergodic invariant measure
(a flow (continuous-time dynamical system) or a cascade) corresponding to a normalized ergodic invariant measure 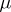
A set of points 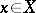 such that:
such that:
a) for every continuous function 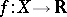 the "time average"
the "time average"
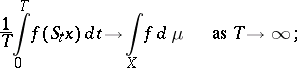 |
b) 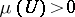 for every neighbourhood
for every neighbourhood 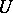 of
of  .
.
A point for which the limit of the time average in a) exists for every continuous 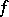 is called quasi-regular. For such a point this limit has the form
is called quasi-regular. For such a point this limit has the form 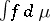 , where
, where  is some normalized invariant measure, depending on
is some normalized invariant measure, depending on  and not necessarily ergodic. If b) holds for this
and not necessarily ergodic. If b) holds for this 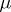 , then the point is called a density point, if this
, then the point is called a density point, if this 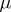 is ergodic, then the point is called transitive; when both conditions hold, the point is called regular. The set of non-regular points has measure zero relative to any normalized invariant measure. The partition of the set of regular points into ergodic sets corresponding to different
is ergodic, then the point is called transitive; when both conditions hold, the point is called regular. The set of non-regular points has measure zero relative to any normalized invariant measure. The partition of the set of regular points into ergodic sets corresponding to different  is the strongest realization of the idea of decomposing a dynamical system into ergodic components (which is valid under stronger restrictions on the system).
is the strongest realization of the idea of decomposing a dynamical system into ergodic components (which is valid under stronger restrictions on the system).
Ergodic sets were introduced by N.N. Bogolyubov and N.M. Krylov [1]. For other accounts, discussions of various generalizations and related questions see the references to Invariant measure 1) and Metric transitivity.
References
| [1] | N. Krylov, N. [N.N. Bogolyubov] Bogoliouboff, "La théorie générale de la mesure dans son application à l'étude des systèmes dynamiques de la mécanique non-linéare" Ann. of Math. Ser. (2) , 38 (1937) pp. 65–113 |
Comments
A good account of ergodic sets is given in [a1]. Closely related is the notion of a generic point (with respect to a normalized invariant measure 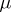 ): A quasi-regular point such that for every continuous
): A quasi-regular point such that for every continuous 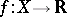 the limit in a) is
the limit in a) is 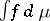 , where
, where 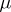 is the given measure.
is the given measure.
References
| [a1] | J.C. Oxtoby, "Ergodic sets" Bull. Amer. Math. Soc. , 58 (1952) pp. 116–136 |
Ergodic set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ergodic_set&oldid=18858