Equivariant estimator
A statistical point estimator that preserves the structure of the problem of statistical estimation relative to a given group of one-to-one transformations of a sampling space.
Suppose that in the realization of a random vector 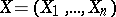 , the components
, the components 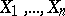 of which are independent, identically distributed random variables taking values in a sampling space
of which are independent, identically distributed random variables taking values in a sampling space 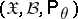 ,
, 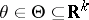 , it is necessary to estimate the unknown true value of the parameter
, it is necessary to estimate the unknown true value of the parameter 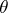 . Next, suppose that on
. Next, suppose that on 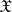 acts a group of one-to-one transformations
acts a group of one-to-one transformations 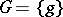 such that
such that
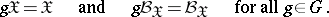 |
In turn, the group 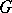 generates on the parameter space
generates on the parameter space 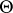 a so-called induced group of transformations
a so-called induced group of transformations 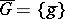 , the elements of which are defined by the formula
, the elements of which are defined by the formula
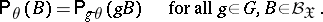 |
Let  be a group of one-to-one transformations on
be a group of one-to-one transformations on 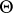 such that
such that
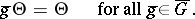 |
Under these conditions it is said that a point estimator 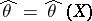 of
of 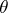 is an equivariant estimator, or that it preserves the structure of the problem of statistical estimation of the parameter
is an equivariant estimator, or that it preserves the structure of the problem of statistical estimation of the parameter 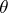 with respect to the group
with respect to the group 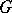 , if
, if
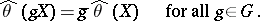 |
The most interesting results in the theory of equivariant estimators have been obtained under the assumption that the loss function is invariant with respect to 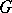 .
.
References
| [1] | S. Zachs, "The theory of statistical inference" , Wiley (1971) |
| [2] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
Equivariant estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equivariant_estimator&oldid=15622