Difference between revisions of "Equivalence problem for systems of second-order ordinary differential equations"
m (AUTOMATIC EDIT (latexlist): Replaced 69 formulas out of 73 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 73 formulas, 69 were replaced by TEX code.--> | Out of 73 formulas, 69 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
Let $( x ^ { 1 } , \ldots , x ^ { n } ) = ( x )$, $( d x ^ { 1 } / d t , \ldots , d x ^ { n } / d t ) = ( d x / d t ) = ( \dot { x } )$, and $t$ be $2 n + 1$ coordinates in an open connected subset $\Omega$ of the Euclidean $( 2 n + 1 )$-dimensional space $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n } \times \mathbf{R} ^ { 1 }$. Suppose that there is given a second-order system | Let $( x ^ { 1 } , \ldots , x ^ { n } ) = ( x )$, $( d x ^ { 1 } / d t , \ldots , d x ^ { n } / d t ) = ( d x / d t ) = ( \dot { x } )$, and $t$ be $2 n + 1$ coordinates in an open connected subset $\Omega$ of the Euclidean $( 2 n + 1 )$-dimensional space $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n } \times \mathbf{R} ^ { 1 }$. Suppose that there is given a second-order system | ||
Latest revision as of 17:47, 1 July 2020
Let $( x ^ { 1 } , \ldots , x ^ { n } ) = ( x )$, $( d x ^ { 1 } / d t , \ldots , d x ^ { n } / d t ) = ( d x / d t ) = ( \dot { x } )$, and $t$ be $2 n + 1$ coordinates in an open connected subset $\Omega$ of the Euclidean $( 2 n + 1 )$-dimensional space $\mathbf{R} ^ { n } \times \mathbf{R} ^ { n } \times \mathbf{R} ^ { 1 }$. Suppose that there is given a second-order system
\begin{equation} \tag{a1} \frac { d ^ { 2 } x ^ { i } } { d t ^ { 2 } } + g ^ { i } ( x , \dot { x } , t ) = 0 , \quad i = 1 , \dots , n, \end{equation}
for which each $g ^ { i }$ is $C ^ { \infty }$ in a neighbourhood of initial conditions $( ( x )_{ 0} , ( \dot { x } ) _ { 0 } , t _ { 0 } ) \in \Omega$.
Following D. Kosambi [a8], one wishes to solve the problem of finding the intrinsic geometric properties (i.e., the basic differential invariants) of (a1) under non-singular coordinate transformations of the type
\begin{equation*} \text{(A)} \left\{ \begin{array} { l } { \overline{x} \square ^ { i } = f ^ { i } ( x ^ { 1 } , \ldots , x ^ { n } ) , \quad i = 1 , \ldots , n, } \\ { \overline { t } = t .} \end{array} \right. \end{equation*}
A similar problem was solved by E. Cartan and S.S. Chern [a4], [a5], but in the real-analytic case with transformations $( \text{A} )$ replaced by
\begin{equation*} (\text{B}) \left\{ \begin{array} { l } { \overline{x} \square ^ { i } = f ^ { i } ( x ^ { 1 } , \ldots , x ^ { n } , t ) , \quad i = 1 , \ldots , n, } \\ { \overline { t } = t. } \end{array} \right. \end{equation*}
Below, only $( \text{A} )$ is considered; see the references for $( \operatorname {B} )$.
Define the KCC-covariant differential of a contravariant vector field $\xi ^ { i } ( x )$ on $\Omega$ by
\begin{equation} \tag{a2} \frac { \mathcal{D} \xi ^ { i } } { d t } = \frac { d \xi ^ { i } } { d t } + \frac { 1 } { 2 } g ^ { i } ;r \xi ^ { r }, \end{equation}
where the semi-colon indicates partial differentiation with respect to $\dot { x } \square ^ { r }$. Note that the Einstein summation convention on repeated upper and lower indices is used throughout. Using (a2), equation (a1) can be re-expressed as
\begin{equation} \tag{a3} \frac { \mathcal{D} \dot { x } ^ { i } } { d t } = \varepsilon ^ { i } = \frac { 1 } { 2 } g ^ { i } ; r \dot { x } \square ^ { r } - g ^ { i }. \end{equation}
The quantity $\varepsilon ^ { i }$ is a contravariant vector field on $\Omega$ and constitutes the first KCC-invariant of (a1). It represents an "external force" .
If the trajectories $x ^ { i } ( t )$ of (a1) are varied into nearby ones according to
\begin{equation} \tag{a4} \bar{x} \square ^ { i } ( t ) = x ^ { i } ( t ) + \xi ^ { i } ( t ) \eta, \end{equation}
where $ \eta $ denotes a constant with $| \eta |$ small and the $\xi ^ { i } ( t )$ are the components of some contravariant vector defined along $x ^ { i } = x ^ { i } ( t )$, substitution of (a4) into (a1) and taking the limit as $\eta \rightarrow 0$ results in the variational equations
\begin{equation} \tag{a5} \frac { d ^ { 2 } \xi ^ { i } } { d t ^ { 2 } } + g _ { ; r } ^ { i } \frac { d \xi ^ { r } } { d t } + g _ {, r } ^ { i } \xi ^ { r } = 0, \end{equation}
where the comma indicates partial differentiation with respect to $x ^ { r }$. Using the KCC-covariant differential (a2), this can be re-expressed as
\begin{equation} \tag{a6} \frac { \mathcal{D} ^ { 2 } \xi ^ { i } } { d t ^ { 2 } } = \mathcal{P} _ { r } ^ { i } \xi ^ { r }, \end{equation}
where
\begin{equation} \tag{a7} \mathcal{P} _ { j } ^ { i } = \end{equation}
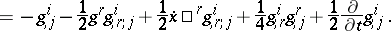 |
The tensor $\mathcal{P} _ { j } ^ { i }$ is the second KCC-invariant of (a1). The third, fourth and fifth invariants are:
 | (a8) |
The main result of KCC-theory is the following assertion: Two systems of the form (a1) on $\Omega$ are equivalent relative to $( \text{A} )$ if and only if the five KCC-invariant tensors $\varepsilon ^ { i }$, $\mathcal{P} _ { j } ^ { i }$, $\mathcal{R} _ { j k } ^ { i }$, $\mathcal{B} _ { j k \text{l}} ^ { i }$, and $\mathcal{D} _ { j k \text{l} } ^ { i }$ are equivalent. In particular, there exist coordinates $( \bar{x} )$ for which the $g ^ { i } ( \bar{x} , \dot { \bar{x} } , t )$ all vanish if and only if all KCC-invariants are zero.
Remarks.
$\varepsilon ^ { i } = 0$ if and only if $g ^ { i } ( x , \dot { x } , t )$ are positively homogeneous of degree two in the variable $\dot { x } ^ { i }$. In this case, the structure of $\Omega$ must accommodate possible non-differentiability in $\dot { x } \square ^ { i }$. This happens in Finsler geometry, but not in affine and Riemannian geometries, where (a1) are geodesics or autoparallels of a linear connection whose coefficients are $g ^ { i }_{ ; j ; k } / 2$. The latter are known as the coefficients of the Berwald connection in Finsler geometry, and of the Levi-Civita connection for Riemannian theory [a3], [a9], [a10]. Furthermore, in the Finsler case, $\mathcal{R} _ { j k } ^ { i }$, $\mathcal{B} _ { j k \text{l}} ^ { i }$ are the Berwald torsion and curvature tensors. Also, $\mathcal{D} _ { j k \text{l} } ^ { i }$ is the Douglas tensor, whose vanishing is necessary and sufficient for all $g ^ { i }$ to be quadratic in the variables $\dot { x } \square ^ { i }$. The latter is always zero in Riemannian and affine geometries, and also for Berwald spaces in Finsler theory [a6], [a3].
Finally, the KCC-invariants can be readily computed in each of the two following cases:
1)
\begin{equation*} \ddot { x } + p \dot { x } + q x = 0, \end{equation*}
where $p$, $q$ are $C ^ { \infty }$ functions of $t$ only. In this case $\varepsilon \neq 0$ and
\begin{equation*} {\cal P} _ { 1 } ^ { 1 } = \frac { 1 } { 4 } p ^ { 2 } + \frac { 1 } { 2 } \dot { p } - q = I. \end{equation*}
The trajectories of this equation are Lyapunov stable if $I < 0$, and unstable if $I \geq 0$;
2)
\begin{equation*} \frac { d ^ { 2 x ^ { i } } } { d t ^ { 2 } } + \gamma ^ { i_{ j k} } ( x ) \frac { d x ^ { j } } { d t } \frac { d x ^ { k } } { d t } = \lambda _ { ( i ) } \frac { d x ^ { i } } { d t }, \end{equation*}
where $\gamma _ { j k } ^ { i }$ are the coefficients of the Levi-Civita connection of a two-dimensional Riemannian metric, $\lambda _ { i }$ are fixed constants and where the bracket on the right-hand side indicates no summation, [a3]. The KCC-invariants in the case where $\lambda _ { 1 } = \lambda _ { 2 }$ are close to Riemannian, but $\lambda _ { 1 } \neq \lambda _ { 2 }$ has a significant effect on Lyapunov stability.
Further applications of KCC-theory can be found in [a2], [a1]. The equivalence problem can be found in a more general context in [a7], [a11].
References
| [a1] | P.L. Antonelli, P. Auger, "Aggregation and emergence in population dynamics" Math. Compt. Mod. , 27 : 4 (1998) (Edited volume) |
| [a2] | P.L. Antonelli, R.H. Bradbury, "Volterra–Hamilton models in the ecology and evolution of colonial organisms" , World Sci. (1996) |
| [a3] | P.L. Antonelli, R.S. Ingarden, M. Matsumoto, "The theory of sprays and finsler spaces with applications in physics and biology" , Kluwer Acad. Publ. (1993) pp. 350 |
| [a4] | E. Cartan, "Observations sur le mémoire précédent" Math. Z. , 37 (1933) pp. 619–622 |
| [a5] | S. Chern, "Sur la géométrie d'un système d'équations differentielles du second ordre" Bull. Sci. Math. II , 63 (1939) pp. 206–212 (Also: Selected Papers, Vol. II, Springer 1989, 52–57) |
| [a6] | J. Douglas, "The general geometry of paths" Ann. of Math. , 29 (1928) pp. 143–169 |
| [a7] | R.B. Gardner, "The method of equivalence and its application" , CBMS , 58 , SIAM (Soc. Industrial Applied Math.) (1989) |
| [a8] | D. Kosambi, "Parallelism and path-spaces" Math. Z. , 37 (1933) pp. 608–618 |
| [a9] | E. Kreyszig, "Introduction to differential and Riemannian geometry" , Univ. Toronto Press (1968) |
| [a10] | D. Laugwitz, "Differential and Riemannian geometry" , Acad. Press (1965) |
| [a11] | P.J. Olver, "Equivalence, invariants, and symmetry" , Cambridge Univ. Press (1995) |
| [a12] | D. Kosambi, "Systems of differential equations of second order" Quart. J. Math. Oxford , 6 (1935) pp. 1–12 |
Equivalence problem for systems of second-order ordinary differential equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equivalence_problem_for_systems_of_second-order_ordinary_differential_equations&oldid=50411