Epsilon-entropy
of a set in a metric space
The logarithm to the base 2 of the smallest number of points in an  -net for this set. In other words, the
-net for this set. In other words, the  -entropy
-entropy 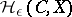 of a set
of a set 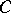 lying in a metric space
lying in a metric space 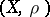 is
is
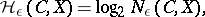 |
where
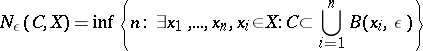 |
and 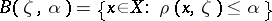 is a ball of radius
is a ball of radius 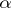 with centre at
with centre at 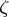 . The definition of
. The definition of  was given by A.N. Kolmogorov in [1], motivated by ideas and definitions of information theory (cf. Information theory).
was given by A.N. Kolmogorov in [1], motivated by ideas and definitions of information theory (cf. Information theory). 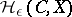 is also called the relative
is also called the relative  -entropy; it depends on the space
-entropy; it depends on the space 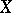 in which the set
in which the set 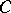 is situated, that is, on the metric extension of
is situated, that is, on the metric extension of 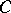 . The quantity
. The quantity
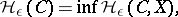 |
where the infimum is taken over all metric extensions 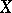 of
of 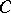 , is called the absolute
, is called the absolute  -entropy of
-entropy of 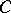 . It may also be defined directly (Kolmogorov, [1]): for a metric space
. It may also be defined directly (Kolmogorov, [1]): for a metric space 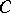 ,
, 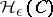 is the logarithm to the base 2 of the cardinality
is the logarithm to the base 2 of the cardinality 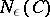 of the most economic (by the number of sets)
of the most economic (by the number of sets) 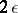 -covering of
-covering of 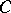 . Here a system of sets
. Here a system of sets 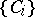 is called a
is called a 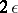 -covering of
-covering of 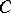 if
if 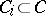 ,
, 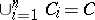 and the diameter of each set does not exceed
and the diameter of each set does not exceed 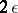 . It has been shown [2] that the absolute
. It has been shown [2] that the absolute  -entropy is the minimum relative
-entropy is the minimum relative  -entropy. The quantities
-entropy. The quantities 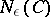 and
and 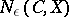 are inverse to the widths (cf. Width)
are inverse to the widths (cf. Width) 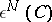 and
and 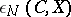 . This characterizes the fact that it is possible to recover the elements of
. This characterizes the fact that it is possible to recover the elements of 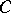 from tables of
from tables of 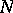 elements and to approximate by
elements and to approximate by 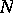 -point sets.
-point sets.
The investigation of the asymptotic behaviour of the  -entropy of various function classes is a special branch of approximation theory.
-entropy of various function classes is a special branch of approximation theory.
References
| [1] | A.N. Kolmogorov, "On certain asymptotic characteristics of completely bounded metric spaces" Dokl. Akad. Nauk SSSR , 108 : 3 (1956) pp. 385–388 (In Russian) |
| [2] | A.G. Vitushkin, "Theory of transmission and processing of information" , Pergamon (1961) (Translated from Russian) |
| [3] | A.N. Kolmogorov, V.M. Tikhomirov, " -entropy and -entropy and  -capacity of sets in functional spaces" Amer. Math. Soc. Transl. Ser. 2 , 17 (1961) pp. 277–364 Uspekhi Mat. Nauk , 14 : 2 (1959) pp. 3–86 -capacity of sets in functional spaces" Amer. Math. Soc. Transl. Ser. 2 , 17 (1961) pp. 277–364 Uspekhi Mat. Nauk , 14 : 2 (1959) pp. 3–86 |
Comments
Kolmogorov's original definition was formulated to investigate the question of whether functions of 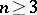 variables are representable as compositions of functions of
variables are representable as compositions of functions of 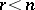 variables. This has a great deal to do with Hilbert's 13th problem, cf. [2] and [a1].
variables. This has a great deal to do with Hilbert's 13th problem, cf. [2] and [a1].
The notion of  -entropy has also proved useful in probability theory, cf. [a2]. It is also called metric entropy.
-entropy has also proved useful in probability theory, cf. [a2]. It is also called metric entropy.
The  -entropy
-entropy 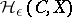 is defined by considering coverings of
is defined by considering coverings of 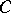 by
by  -balls. An
-balls. An  -packing
-packing 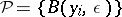 of
of 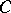 is a collection of
is a collection of  -balls such that
-balls such that 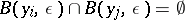 if
if 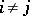 and
and 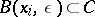 . Let
. Let 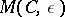 be the maximum cardinality of a packing in
be the maximum cardinality of a packing in 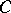 . Then
. Then 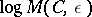 is called the
is called the  -capacity of
-capacity of 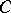 in
in 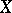 .
.
There are a number of additional (but not unrelated) notions of  -entropy for random variables and random processes. They are defined as follows. Let
-entropy for random variables and random processes. They are defined as follows. Let 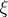 be a random variable with values in a metric space
be a random variable with values in a metric space 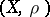 . Let
. Let 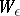 be the set of all random variables
be the set of all random variables 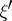 with values in
with values in 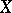 such that
such that 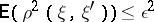 , where
, where 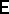 denotes mathematical expectation. Then the
denotes mathematical expectation. Then the  -entropy of
-entropy of 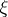 is ([a3])
is ([a3])
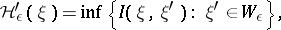 |
where 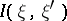 is the usual information function for a pair of random variables (cf. Information). This idea can be easily extended to random processes
is the usual information function for a pair of random variables (cf. Information). This idea can be easily extended to random processes 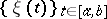 by regarding such a process as a random variable with values in
by regarding such a process as a random variable with values in 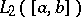 , say. [a4] contains some asymptotic estimates of
, say. [a4] contains some asymptotic estimates of 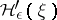 .
.
Now let 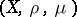 be a probabilistic metric space, i.e.
be a probabilistic metric space, i.e. 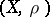 is a metric space and
is a metric space and 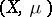 is a probability space. For
is a probability space. For 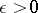 , let
, let 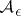 be the set of all partitions of
be the set of all partitions of 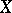 (cf. Decomposition) into measurable sets of diameter
(cf. Decomposition) into measurable sets of diameter 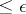 . Then ([a5]) one defines
. Then ([a5]) one defines
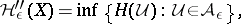 |
where 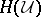 denotes the ordinary entropy of the partition
denotes the ordinary entropy of the partition 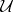 . Define
. Define
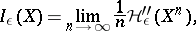 |
where 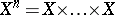 (
( factors) with the product measure and distance. (This limit exists.) For a measure
factors) with the product measure and distance. (This limit exists.) For a measure 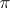 on
on 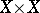 such that
such that 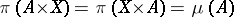 for all measurable
for all measurable 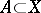 , let
, let
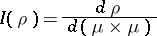 |
be the Radon–Nikodým derivative. Let 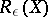 be the set of all measures
be the set of all measures 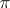 on the measurable space
on the measurable space 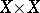 such that
such that 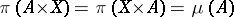 for
for 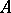 measurable and
measurable and
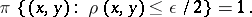 |
Then
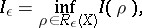 |
which is a noisy channel coding theorem; cf. [a6]. There are also estimates both ways relating 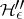 and
and 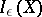 ; cf. [a6]. Cf. also [a7] for (more) relations between
; cf. [a6]. Cf. also [a7] for (more) relations between 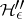 and (extended notions of) Shannon entropy.
and (extended notions of) Shannon entropy.
Define the absolute  -entropy
-entropy 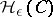 (as in the main article above) by means of
(as in the main article above) by means of  -partitions of
-partitions of 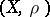 by means of Borel sets. Then
by means of Borel sets. Then
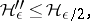 |
but it need not be true that the supremum of the 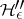 for varying
for varying 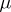 on
on 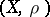 is equal to
is equal to 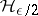 , cf. [a5].
, cf. [a5].
Now let again 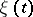 ,
, 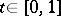 , be a stochastic Gaussian process (real-valued), let
, be a stochastic Gaussian process (real-valued), let 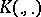 be its covariance function and let
be its covariance function and let 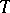 be the integral operator with kernel
be the integral operator with kernel 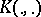 , i.e.
, i.e.
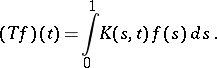 |
Let 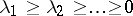 be the eigen values of
be the eigen values of 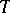 . For
. For 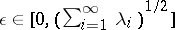 define a function
define a function 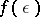 by the equality
by the equality
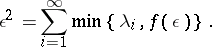 |
Then Pinsker's theorem says that
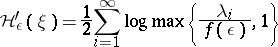 |
(where log stands for the logarithm to the base 2). One also has ([a8]): For all 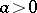 ,
,
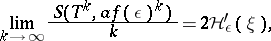 |
where for a suitable operator on a Hilbert space 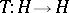 the entropy
the entropy  is defined as the metric entropy of the set
is defined as the metric entropy of the set 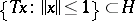 :
:
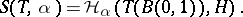 |
References
| [a1] | G.G. Lorentz, "The 13-th problem of Hilbert" F.E. Browder (ed.) , Mathematical developments arising from Hilbert problems , Proc. Symp. Pure Math. , 28 , Amer. Math. Soc. (1976) pp. 419–430 |
| [a2] | R.M. Dudley, "Metric entropy and the central limit theorem in 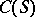 " Ann. Inst. Fourier (Grenoble) , 24 (1974) pp. 49–60 " Ann. Inst. Fourier (Grenoble) , 24 (1974) pp. 49–60 |
| [a3] | A.N. Kolmogorov, "Theory of transmission of information" Amer. Math. Soc. Transl. Ser. 2 , 33 (1963) pp. 291–321 Acad. R. P. Romine An. Romino-Sov. , 13 : 1 (1959) pp. 5–33 |
| [a4] | J. Biria, M. Zakai, J. Ziv, "On the  -entropy and the rate distortion function of certain non-Gaussian processes" IEEE Trans. Inform. Theory , 20 (1974) pp. 517–524 -entropy and the rate distortion function of certain non-Gaussian processes" IEEE Trans. Inform. Theory , 20 (1974) pp. 517–524 |
| [a5] | E.C. Posner, E.R. Rodenich, H. Rumsey, " -Entropy of stochastic processes" Ann. Math. Stat. , 38 (1967) pp. 1000–1020 -Entropy of stochastic processes" Ann. Math. Stat. , 38 (1967) pp. 1000–1020 |
| [a6] | E.C. Posner, E.R. Rodenich, "Epsilon entropy and data compression" Ann. Math. Stat. , 42 (1971) pp. 2079–2125 |
| [a7] | M. Katětov, "On extended Shannon entropies and the epsilon entropy" Comm. Math. Univ. Carolinae , 27 (1986) pp. 519–534 |
| [a8] | S. Akashi, "On operator theoretical characterization of epsilon-entropy in Gaussian processes" Kodai Math. J. , 9 (1986) pp. 58–67 |
Epsilon-entropy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Epsilon-entropy&oldid=12568