Entropy
An information-theoretical measure of the degree of indeterminacy of a random variable. If 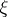 is a discrete random variable defined on a probability space
is a discrete random variable defined on a probability space 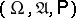 and assuming values
and assuming values 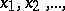 with probability distribution
with probability distribution 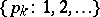 ,
, 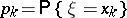 , then the entropy is defined by the formula
, then the entropy is defined by the formula
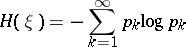 | (1) |
(here it is assumed that 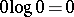 ). The base of the logarithm can be any positive number, but as a rule one takes logarithms to the base 2 or
). The base of the logarithm can be any positive number, but as a rule one takes logarithms to the base 2 or  , which corresponds to the choice of a bit or a nat (natural unit) as the unit of measurement.
, which corresponds to the choice of a bit or a nat (natural unit) as the unit of measurement.
If 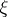 and
and 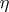 are two discrete random variables taking values
are two discrete random variables taking values 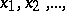 and
and 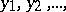 with probability distributions
with probability distributions 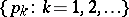 and
and 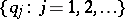 , and if
, and if 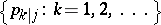 is the conditional distribution of
is the conditional distribution of 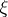 assuming that
assuming that 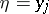 ,
, 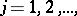 then the (mean) conditional entropy
then the (mean) conditional entropy 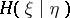 of
of 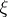 given
given 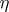 is defined as
is defined as
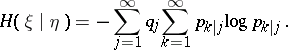 | (2) |
Let 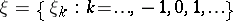 be a stationary process with discrete time and discrete space of values such that
be a stationary process with discrete time and discrete space of values such that 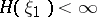 . Then the entropy (more accurately, the mean entropy)
. Then the entropy (more accurately, the mean entropy) 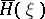 of this stationary process is defined as the limit
of this stationary process is defined as the limit
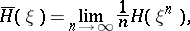 | (3) |
where 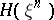 is the entropy of the random variable
is the entropy of the random variable 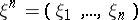 . It is known that the limit on the right-hand side of (3) always exists and that
. It is known that the limit on the right-hand side of (3) always exists and that
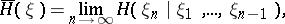 | (4) |
where 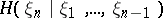 is the conditional entropy of
is the conditional entropy of 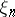 given
given 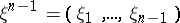 . The entropy of stationary processes has important applications in the theory of dynamical systems.
. The entropy of stationary processes has important applications in the theory of dynamical systems.
If 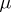 and
and  are two measures on a measurable space
are two measures on a measurable space 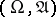 and if
and if 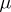 is absolutely continuous relative to
is absolutely continuous relative to  and
and 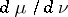 is the corresponding Radon–Nikodým derivative, then the entropy
is the corresponding Radon–Nikodým derivative, then the entropy 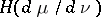 of
of 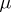 relative to
relative to  is defined as the integral
is defined as the integral
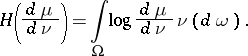 | (5) |
A special case of the entropy of one measure with respect to another is the differential entropy.
Of the many possible generalizations of the concept of entropy in information theory one of the most important is the following. Let 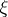 and
and 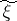 be two random variables taking values in certain measurable spaces
be two random variables taking values in certain measurable spaces 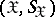 and
and 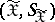 . Suppose that the distribution
. Suppose that the distribution 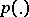 of
of 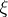 is given and let
is given and let 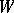 be a class of admissible joint distributions of the pair
be a class of admissible joint distributions of the pair 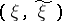 in the set of all probability measures in the product
in the set of all probability measures in the product 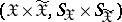 . Then the
. Then the 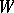 -entropy (or the entropy for a given condition
-entropy (or the entropy for a given condition 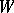 of exactness of reproduction of information (cf. Information, exactness of reproducibility of)) is defined as the quantity
of exactness of reproduction of information (cf. Information, exactness of reproducibility of)) is defined as the quantity
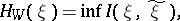 | (6) |
where 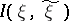 is the amount of information (cf. Information, amount of) in
is the amount of information (cf. Information, amount of) in 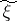 given
given 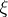 and the infimum is taken over all pairs of random variables
and the infimum is taken over all pairs of random variables 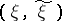 such that the joint distribution
such that the joint distribution 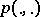 of the pair
of the pair 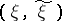 belongs to
belongs to 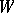 and
and 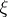 has the distribution
has the distribution 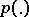 . The class
. The class 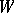 of joint distributions
of joint distributions 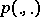 is often given by means of a certain non-negative measurable real-valued function
is often given by means of a certain non-negative measurable real-valued function 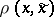 ,
, 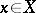 ,
, 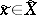 , a measure of distortion, in the following manner:
, a measure of distortion, in the following manner:
 | (7) |
where 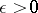 is fixed. In this case the quantity defined by (6), where
is fixed. In this case the quantity defined by (6), where 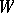 is given by (7), is called the
is given by (7), is called the  -entropy (or the rate as a function of the distortion) and is denoted by
-entropy (or the rate as a function of the distortion) and is denoted by 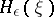 . For example, if
. For example, if 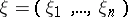 is a Gaussian random vector with independent components, if
is a Gaussian random vector with independent components, if 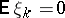 ,
, 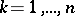 , and if the function
, and if the function 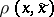 ,
, 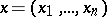 ,
, 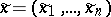 , has the form
, has the form
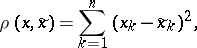 |
then 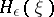 can be found by the formula
can be found by the formula
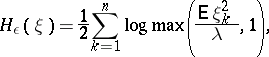 |
where 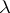 is defined by
is defined by
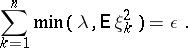 |
If 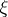 is a discrete random variable, if
is a discrete random variable, if 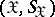 and
and 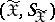 are the same, and if
are the same, and if 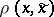 has the form
has the form
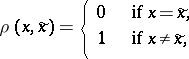 |
then the  -entropy for
-entropy for 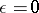 is equal to the ordinary entropy defined in (1), that is,
is equal to the ordinary entropy defined in (1), that is, 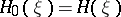 .
.
References
| [1] | C. Shannon, "A mathematical theory of communication" Bell System Techn. J. , 27 (1948) pp. 379–423; 623–656 |
| [2] | R.G. Gallager, "Information theory and reliable communication" , Wiley (1968) |
| [3] | T. Berger, "Rate distortion theory" , Prentice-Hall (1971) |
| [4] | P. Billingsley, "Ergodic theory and information" , Wiley (1956) |
Comments
For entropy in the theory of dynamical systems see Entropy theory of a dynamical system and Topological entropy.
Entropy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Entropy&oldid=15099