Endomorphism ring

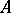The associative ring consisting of all morphisms of into itself, where is an object in some additive category. The multiplication in is composition of morphisms, and addition is the addition of morphisms defined by the axioms of the additive category. The identity morphism is the unit element of the ring . An element in is invertible if and only if is an automorphism of the object . If and 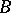are objects of an additive category 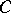, then the group has the natural structure of a right module over and of a left module over . Let be a covariant (or contravariant) additive functor from an additive category into an additive category 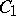. Then for any object in 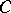the functor induces a natural homomorphism (or anti-homomorphism) .

Let 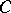be the category of modules over a ring 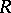. For an -module the ring 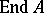consists of all endomorphisms of the Abelian group that commute with multiplication by elements of . The sum of two endomorphism 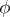and is defined by the formula

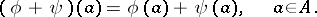If is commutative, then has the natural structure of an 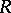-algebra. Many properties of the module can be characterized in terms of . For example, is an irreducible module if and only if is a skew-field.

An arbitrary homomorphism 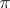of an associative ring into is called a representation of the ring (by endomorphisms of the object ). If has a unit element, then one imposes the additional condition . Any associative ring 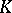has a faithful representation in the endomorphism ring of a certain Abelian group . If , moreover, has a unit element, then can be chosen as the additive group of on which the elements of 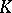act by left multiplication. 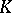If has no unit element and is obtained from by adjoining a unit to externally, then can be taken to be the additive group of .

In the case of an Abelian variety one considers, apart from the ring 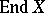, which is a finitely-generated -module, the algebra of endomorphisms (algebra of complex multiplications) .

References

[1]	C. Faith, "Algebra: rings, modules, and categories" , 1–2 , Springer (1973–1976)
[2]	D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974)
[3]	V.T. Markov, A.V. Mikhalev, L.A. Skornyakov, A.A. Tugaubaev, "Endomorphism rings of modules and lattices of submodules" J. Soviet Math. , 31 : 3 (1985) pp. 3005–3051 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 21 (1983) pp. 183–254