Empirical process

A stochastic process constructed from a sample and the corresponding probability measure. Let 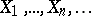be a sequence of independent random elements with common law 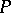, taking values in a measurable space 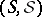. The empirical measure 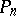of the first 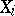s is the discrete random measure that places mass 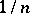on each such :

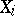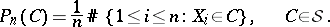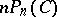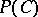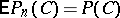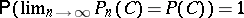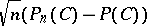Obviously, is binomially distributed with parameters and (cf. Binomial distribution). Hence , , and converges in distribution, as 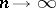, to a centred normal random variable with variance 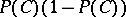(cf. Convergence in distribution). Therefore it is natural to define an empirical process indexed by sets by

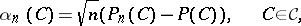(a1)

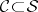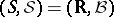where . If and 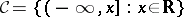, one writes 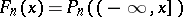for the empirical distribution function, and the empirical process specializes to the classical empirical process

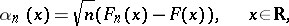(a2)

where 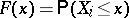, , 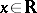is the distribution function of the elements 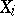. Replacing sets by their indicator functions leads, more generally, to the definition of an empirical process indexed by functions:

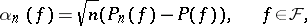(a3)

where

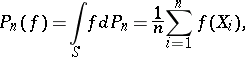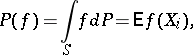and 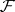is a suitable class of measurable functions from 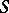to .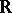

The main aim of the theory of empirical processes is to obtain results uniformly in 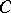, or 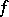; in particular, Glivenko–Cantelli-type theorems, central limit theorems, laws of the iterated logarithm, and probability inequalities (cf., e.g., Empirical distribution; Central limit theorem; Law of the iterated logarithm). (Measurability issues will be disregarded in the sequel.) The concept of a Vapnik–Chervonenkis class plays an important role in set-indexed situations. E.g., if 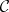is a Vapnik–Chervonenkis class, then for every probability measure 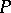on ,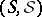

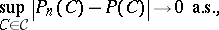(a4)

and 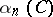, , 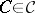converges weakly (see [a10] and Weak topology) to 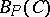, , 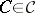a centred, bounded Gaussian process, which is uniformly continuous (with respect to the pseudometric 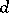defined by 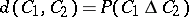) and has covariance structure

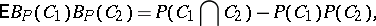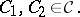For the classical empirical process in (a2), this limiting process specializes to 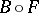, where 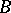is a Brownian bridge (cf. Non-parametric methods in statistics). A sharp version of the first result is the following: (a4) holds if and only if

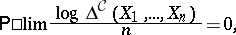(a5)

where

(see Vapnik–Chervonenkis class). A corresponding sharp version of the central limit theorem exists too; essentially the only change is that the in the denominator of (a5) has to be replaced by 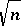to obtain an "if and only if" condition for the central limit theorem. Other useful concepts in connection with empirical processes are various notions of entropy, see [a12], [a13], [a9], [a10]. Also, for the function-indexed process in (a3), the analogues of (a4) and the central limit theorem above have been studied thoroughly, see [a5], [a9], [a10].

For the classical empirical process in (a2), approximation theorems which yield a rate of convergence in the central limit theorem are extremely useful: A sequence of Brownian bridges 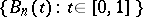, , 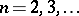can be constructed such that for all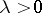

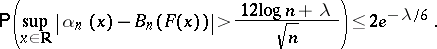A similar, only slightly less sharp, result can be obtained for the situation where the joint distribution of the 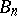s is known, i.e., the 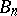s are defined by means of one single Kiefer process, see [a3].

Empirical and related processes have many applications in many different subfields of probability theory and (non-parametric) statistics.

References

[a1]	K.S. Alexander, "Rates of growth and sample moduli for weighted empirical processes indexed by sets" Probab. Th. Rel. Fields , 75 (1987) pp. 379–423
[a2]	M. Csörgő, S. Csörgő, L. Horváth, D.M. Mason, "Weighted empirical and quantile processes" Ann. of Probab. , 14 (1986) pp. 31–85
[a3]	M. Csörgő, P. Révész, "Strong approximations in probability and statistics" , Acad. Press (1981)
[a4]	P. Deheuvels, D.M. Mason, "Functional laws of the iterated logarithm for the increments of empirical and quantile processes" Ann. of Probab. , 20 (1992) pp. 1248–1287
[a5]	R.M. Dudley, "Universal Donsker classes and metric entropy" Ann. of Probab. , 15 (1987) pp. 1306–1326
[a6]	J.H.J. Einmahl, "The a.s. behavior of the weighted empirical process and the LIL for the weighted tail empirical process" Ann. of Probab. , 20 (1992) pp. 681–695
[a7]	E. Giné, "Empirical processes and applications: an overview" Bernoulli , 2 (1996) pp. 1–28
[a8]	P. Massart, "The tight constant in the Dvoretzky–Kiefer–Wolfowitz inequality" Ann. of Probab. , 18 (1990) pp. 1269–1283
[a9]	D. Pollard, "Convergence of stochastic processes" , Springer (1984)
[a10]	A. Sheehy, J.A. Wellner, "Uniform Donsker classes of functions" Ann. of Probab. , 20 (1992) pp. 1983–2030
[a11]	G.R. Shorack, J.A. Wellner, "Empirical processes with applications to statistics" , Wiley (1986)
[a12]	K.S. Alexander, "Probability inequalities for empirical processes and a law of the iterated logarithm" Ann. of Probab. , 12 (1984) pp. 1041–1067
[a13]	K.S. Alexander, "Correction: Probability inequalities for empirical processes and a law of the iterated logarithm" Ann. of Probab. , 15 (1987) pp. 428–430