Elliptic operator
A linear differential or pseudo-differential operator with an invertible principal symbol (see Symbol of an operator).
Let 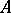 be a differential or pseudo-differential (as a rule, matrix) operator on a domain
be a differential or pseudo-differential (as a rule, matrix) operator on a domain 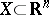 with principal symbol
with principal symbol 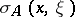 . If
. If  is of order
is of order 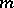 , then
, then 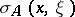 is a matrix-valued function on
is a matrix-valued function on 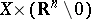 and is positively homogeneous of order
and is positively homogeneous of order 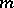 in the variable
in the variable 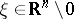 . Then ellipticity means that
. Then ellipticity means that 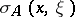 is an invertible matrix for all
is an invertible matrix for all 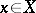 ,
,  . This concept is called Petrovskii ellipticity.
. This concept is called Petrovskii ellipticity.
Another form, Douglis–Nirenberg ellipticity, assumes that 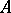 is a matrix-valued operator,
is a matrix-valued operator, 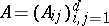 where
where 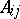 is an operator of order
is an operator of order 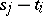 , where
, where 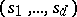 and
and 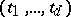 are collections of real numbers. Then one can form the matrix of principal symbols
are collections of real numbers. Then one can form the matrix of principal symbols 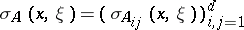 , where the function
, where the function 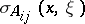 is positively homogeneous in
is positively homogeneous in 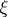 of order
of order 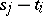 . Now Douglis–Nirenberg ellipticity means that the matrix
. Now Douglis–Nirenberg ellipticity means that the matrix 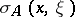 is invertible for all
is invertible for all 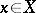 ,
, 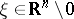 .
.
Ellipticity of an operator 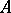 on a manifold means that the operators obtained from it when it is written in local coordinates are elliptic. Equivalently, this ellipticity can be described as invertibility of the principal symbol
on a manifold means that the operators obtained from it when it is written in local coordinates are elliptic. Equivalently, this ellipticity can be described as invertibility of the principal symbol 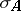 , which is a function on
, which is a function on 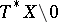 , where
, where 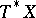 is the cotangent bundle to
is the cotangent bundle to 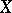 and
and 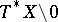 is the same bundle without the zero section. If
is the same bundle without the zero section. If 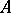 maps the sections of a vector bundle
maps the sections of a vector bundle 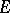 to the sections of another vector bundle
to the sections of another vector bundle 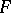 , i.e.
, i.e. 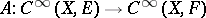 , then ellipticity of the operator means invertibility of the linear operator
, then ellipticity of the operator means invertibility of the linear operator 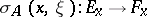 for any point
for any point 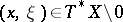 . (Here
. (Here 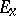 and
and 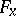 are the fibres of
are the fibres of 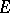 and
and 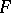 at
at  .) An example of an elliptic operator is the Laplace operator.
.) An example of an elliptic operator is the Laplace operator.
Ellipticity of an operator is equivalent to the absence of real characteristic directions. It can also be understood micro-locally. Namely, ellipticity of an operator 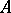 at a point
at a point 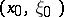 means invertibility of the matrix (linear transformation)
means invertibility of the matrix (linear transformation) 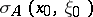 .
.
Ellipticity of a pseudo-differential operator on a manifold with boundary (for example, an operator from the Boutet de Monvel algebra, [10], [11]) at a boundary point means invertibility of a certain model operator of a boundary value problem on a semi-axis. This model operator is obtained from the original one by straightening the boundary, freezing the principal parts of the operator and the boundary conditions at the point in question, and taking the Fourier transform in the tangential directions (from 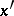 to
to 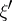 ) with subsequent fixing the non-zero vector
) with subsequent fixing the non-zero vector 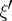 , which can be regarded as a cotangent vector to the boundary. In the case of a differential operator and differential boundary conditions the condition of ellipticity just described can be expressed in algebraic terms. In this (and sometimes also in a general) case this condition is often called the Shapiro–Lopatinskii condition or the condition of coerciveness.
, which can be regarded as a cotangent vector to the boundary. In the case of a differential operator and differential boundary conditions the condition of ellipticity just described can be expressed in algebraic terms. In this (and sometimes also in a general) case this condition is often called the Shapiro–Lopatinskii condition or the condition of coerciveness.
The most characteristic properties of an elliptic operator are: 1) regularity of the solutions of the corresponding equations; 2) accurate a priori estimates; and 3) the Fredholm property of elliptic operators on compact manifolds.
Henceforth, for simplicity, the coefficients and symbols of all operators are assumed to be infinitely smooth.
Let 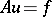 be an equation, where
be an equation, where 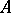 is an elliptic operator. The simplest regularity property is as follows: If
is an elliptic operator. The simplest regularity property is as follows: If 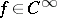 , then
, then 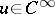 . This holds for arbitrary elliptic differential operators with smooth coefficients or arbitrary elliptic pseudo-differential operators (with smooth symbols). It is also true for elliptic operators of a boundary value problem (that is, it is true up to the boundary when the Shapiro–Lopatinskii condition holds). A sharper form of this property is a micro-local version of it: If
. This holds for arbitrary elliptic differential operators with smooth coefficients or arbitrary elliptic pseudo-differential operators (with smooth symbols). It is also true for elliptic operators of a boundary value problem (that is, it is true up to the boundary when the Shapiro–Lopatinskii condition holds). A sharper form of this property is a micro-local version of it: If 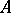 is an elliptic operator at a point
is an elliptic operator at a point 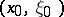 (where
(where 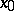 is an interior point of
is an interior point of 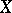 ) and
) and 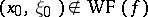 , where
, where  denotes the wave front (of a distribution or a function), then
denotes the wave front (of a distribution or a function), then 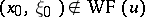 . Another improvement: If
. Another improvement: If 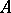 is an elliptic operator of order
is an elliptic operator of order 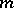 and
and 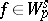 , then
, then 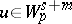 , where
, where 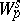 is the Sobolev space,
is the Sobolev space, 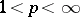 . If
. If 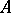 is an elliptic differential operator with analytic coefficients and if
is an elliptic differential operator with analytic coefficients and if 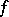 is analytic, then so is
is analytic, then so is  . (In the case of equations with constant coefficients, this property is necessary and sufficient for ellipticity.) The corresponding micro-local version is also valid and can be phrased in the language of analytic wave fronts.
. (In the case of equations with constant coefficients, this property is necessary and sufficient for ellipticity.) The corresponding micro-local version is also valid and can be phrased in the language of analytic wave fronts.
A local a priori estimate for an elliptic operator 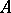 of order
of order 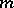 has the form
has the form
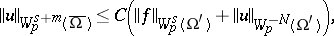 | (1) |
where 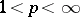 ,
,  ,
, 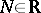 ,
,  and
and 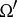 are two domains in
are two domains in 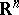 ,
,  is a compact part of
is a compact part of 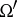 ,
, 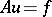 in
in 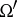 , and the constant
, and the constant 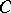 does not depend on
does not depend on  (but may depend on
(but may depend on  ,
,  ,
, 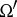 , and
, and 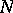 ).
).
A global a priori estimate for an elliptic operator 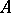 of order
of order 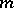 on a compact manifold
on a compact manifold 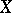 without boundary has the same form as (1), but with
without boundary has the same form as (1), but with  and
and 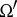 replaced by
replaced by 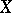 . In the case of a manifold with boundary one has to take instead of the norm of
. In the case of a manifold with boundary one has to take instead of the norm of 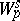 in (1) norms that take account of the structure of the vector-valued functions
in (1) norms that take account of the structure of the vector-valued functions  and
and 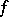 (which contain, generally speaking, boundary components). Suppose, for example, that on a compact manifold
(which contain, generally speaking, boundary components). Suppose, for example, that on a compact manifold 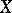 with boundary
with boundary 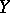 an elliptic operator of the form
an elliptic operator of the form 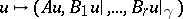 has been given, where
has been given, where 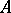 is an elliptic differential operator of order
is an elliptic differential operator of order 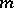 , the
, the 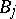 are differential operators of order
are differential operators of order 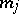 with
with 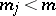 , and suppose that the Shapiro–Lopatinskii condition holds (for
, and suppose that the Shapiro–Lopatinskii condition holds (for 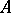 and the system of boundary operators
and the system of boundary operators 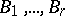 ). Then an a priori estimate in the Sobolev spaces
). Then an a priori estimate in the Sobolev spaces 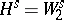 has the form
has the form
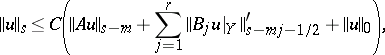 |
where 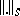 is the norm in
is the norm in 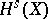 ,
,  that in
that in 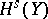 ,
, 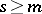 ,
,  , and the constant
, and the constant 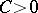 does not depend on
does not depend on  (but may depend on
(but may depend on 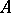 ,
, 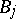 ,
,  ,
, 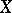 ,
, 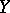 , and the choice of the norm in the Sobolev spaces).
, and the choice of the norm in the Sobolev spaces).
An elliptic operator on a compact manifold (possibly with boundary) determines a Fredholm operator in the corresponding Sobolev spaces, and also in the space of infinitely-differentiable functions. Its index depends only on the principal symbol and does not change under continuous deformations of it. This allows one to raise the problem of calculating the index (see Index formulas).
Elliptic operators with a parameter play an important role (see [12]). When the conditions of ellipticity with a parameter hold on a compact manifold for parameter values of large modulus, then the elliptic operator in question turns out to be invertible, and in the global a priori estimate of the type (1) the last term (the low norm at the right-hand side) can be omitted.
References
| [1] | I.G. [I.G. Petrovskii] Petrowski, "Vorlesungen über partielle Differentialgleichungen" , Teubner (1965) (Translated from Russian) |
| [2] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [3] | O.A. Ladyzhenskaya, N.N. Ural'tseva, "Linear and quasilinear elliptic equations" , Acad. Press (1968) (Translated from Russian) |
| [4] | J.L. Lions, E. Magenes, "Non-homogenous boundary value problems and applications" , 1–2 , Springer (1972) (Translated from French) |
| [5] | L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964) |
| [6] | S. Agmon, A. Douglis, L. Nirenberg, "Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions" Comm. Pure Appl. Math. , 12 (1959) pp. 623–627 |
| [7] | L. Hörmander, "Linear partial differential equations" , Springer (1963) |
| [8] | M.A. Shubin, "Pseudo-differential operators and spectral theory" , Springer (1987) (Translated from Russian) |
| [9] | R.S. Palais, "Seminar on the Atiyah–Singer index theorem" , Princeton Univ. Press (1965) |
| [10] | B.W. Schulze, "Index theory of elliptic boundary problems" , Akademie Verlag (1982) |
| [11] | L. Boutet de Monvel, "Boundary problems for pseudo-differential operators" Acta Math. , 126 (1971) pp. 11–51 |
| [12] | M.S. Agranovich, M.I. Vishik, "Elliptic problems with a parameter and parabolic problems of general type" Russian Math. Surveys , 19 (1964) pp. 53–157 Uspekhi Mat. Nauk , 19 : 3 (1964) pp. 53–161 |
Comments
Boundary value problems for elliptic differential operators can be reduced to systems of pseudo-differential equations on the boundary, the advantage being that the latter is a manifold without boundary. These systems involve the so-called Calderón projection in the space of Cauchy data, this is related to the Hilbert transform in the case of the Cauchy–Riemann operator in the complex plane. Cf. [a1].
[a1] is part of a  -volume treatise which grew out of [7].
-volume treatise which grew out of [7].
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 3 , Springer (1985) |
Elliptic operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_operator&oldid=13172