Elliptic function
in the proper sense
A double-periodic function that is meromorphic in the finite complex  -plane. An elliptic function has the following basic properties.
-plane. An elliptic function has the following basic properties.
There are no entire elliptic functions except the constants (Liouville's theorem).
Let  be the primitive periods of an elliptic function
be the primitive periods of an elliptic function  ,
, 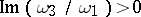 (cf. Double-periodic function). The sum of the residues of all poles of
(cf. Double-periodic function). The sum of the residues of all poles of  in its period parallelogram
in its period parallelogram
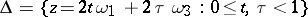 |
is zero.
Let  be the number of poles (counted with multiplicities) of an elliptic function
be the number of poles (counted with multiplicities) of an elliptic function  in a period parallelogram
in a period parallelogram  . Then
. Then 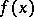 takes in
takes in 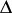 every finite value exactly
every finite value exactly  times, counted with multiplicities. The number
times, counted with multiplicities. The number  is called the order of
is called the order of 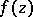 . There are no elliptic functions of order less than 2.
. There are no elliptic functions of order less than 2.
If 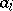 and
and 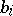 ,
, 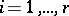 , are all the zeros and poles of an elliptic function
, are all the zeros and poles of an elliptic function 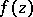 in a period parallelogram
in a period parallelogram 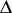 , counted with multiplicities, then the sum
, counted with multiplicities, then the sum
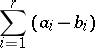 |
is congruent to zero modulo the periods, that is,
 |
where 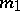 and
and 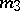 are integers (a special case of Abel's theorem, see Abelian function).
are integers (a special case of Abel's theorem, see Abelian function).
All the elliptic functions with fixed primitive periods 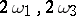 form an algebraic field of elliptic functions with two generators. For these generators one can take, for example, the Weierstrass
form an algebraic field of elliptic functions with two generators. For these generators one can take, for example, the Weierstrass 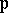 -function and its derivative (see Weierstrass elliptic functions).
-function and its derivative (see Weierstrass elliptic functions).
The derivative of an elliptic function is itself an elliptic function, having the same periods. Every elliptic function satisfies a first-order ordinary differential equation. Every elliptic function 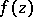 satisfies an algebraic addition theorem, that is, the values
satisfies an algebraic addition theorem, that is, the values 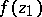 ,
, 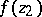 and
and 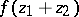 are connected by an irreducible algebraic equation with constant coefficients. Conversely, Weierstrass' theorem asserts that every analytic function
are connected by an irreducible algebraic equation with constant coefficients. Conversely, Weierstrass' theorem asserts that every analytic function 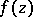 admitting an algebraic addition theorem is either a rational function of
admitting an algebraic addition theorem is either a rational function of  or of
or of 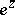 , or is an elliptic function.
, or is an elliptic function.
Sometimes a more general terminology is used, connected with the theory of theta-functions (cf. Theta-function). An elliptic function of the third kind is defined to be any meromorphic function 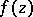 satisfying a functional equation
satisfying a functional equation
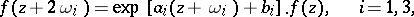 |
where 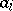 and
and 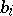 are constants. If
are constants. If 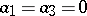 , it is called an elliptic function of the second kind. If
, it is called an elliptic function of the second kind. If  , then
, then 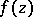 is said to be of the first kind, or an elliptic function in the proper sense. In this terminology the Jacobi theta-functions (see Jacobi elliptic functions) and the Weierstrass
is said to be of the first kind, or an elliptic function in the proper sense. In this terminology the Jacobi theta-functions (see Jacobi elliptic functions) and the Weierstrass 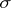 -function (see Weierstrass elliptic functions) are of the third kind.
-function (see Weierstrass elliptic functions) are of the third kind.
Elliptic integrals (cf. Elliptic integral) were first investigated in works of scholars at the end of the 17th century to the beginning of the 19th century: Jacob Bernoulli, and Johann Bernoulli, G.C. Fagnano dei Toschi, L. Euler, and A. Legendre. These integrals appeared in the problems of computing the arc length of an ellipse and other conics. They have the form 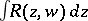 , where
, where 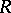 is a rational function in variables
is a rational function in variables  and
and 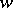 connected by an algebraic equation
connected by an algebraic equation
 |
in which the right-hand side is a polynomial of degree 4 or 3 without multiple roots. The integrand is single-valued on a two-sheeted compact Riemann surface 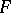 of genus 1 with four branch points. The differentials of the first, second and third kind on
of genus 1 with four branch points. The differentials of the first, second and third kind on 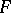 (see Differential on a Riemann surface) generate elliptic integrals of the first, second and third kind, respectively. An integral of the first kind is a principal uniformizing function for
(see Differential on a Riemann surface) generate elliptic integrals of the first, second and third kind, respectively. An integral of the first kind is a principal uniformizing function for 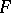 and for the algebraic function field generated by
and for the algebraic function field generated by 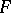 . If one takes it as an independent variable, then this field becomes a field of elliptic functions.
. If one takes it as an independent variable, then this field becomes a field of elliptic functions.
The idea of a direct inversion of an elliptic integral in Legendre normal form originated and was developed in work of N.H. Abel and C.G.J. Jacobi at the beginning of the 19th century. The construction of elliptic functions on the basis of theta-functions, developed by Jacobi, is of fundamental importance in applications of elliptic functions. The theoretically simpler construction of the field of elliptic functions in which one takes as generators the function 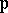 and its derivative was made by K. Weierstrass in the 1870s.
and its derivative was made by K. Weierstrass in the 1870s.
One of the basic problems in the development of the theory of elliptic functions was the problem of transformation of elliptic functions and related quantities on transition from primitive periods 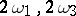 to other primitive periods
to other primitive periods 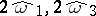 connected by relations
connected by relations
 |
where 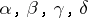 are integers such that
are integers such that 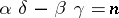 , where
, where  is natural number, the so-called order of the transformation. The area of the period parallelogram of
is natural number, the so-called order of the transformation. The area of the period parallelogram of 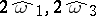 is
is  times larger than that of the period parallelogram of
times larger than that of the period parallelogram of 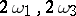 . For
. For 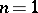 one obtains the transformations of the modular group, which gave rise to the theory of modular functions (cf. Modular function), connected with that of elliptic functions.
one obtains the transformations of the modular group, which gave rise to the theory of modular functions (cf. Modular function), connected with that of elliptic functions.
Elliptic functions can be treated as meromorphic functions that are invariant under transformations of the translation group
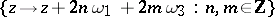 |
of the complex plane. A generalization of this approach led to the consideration of automorphic functions (cf. Automorphic function), which are invariant under fractional-linear transformations (cf. Fractional-linear mapping), which form a group of a more general kind. Elliptic and modular functions are special cases of automorphic functions.
The inversion of elliptic integrals led straight to the Jacobi inversion problem for more general Abelian integrals (cf. Abelian integral)  , where the variables
, where the variables  and
and 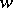 are connected by an arbitrary algebraic equation. Along these lines one obtains the Abelian functions (cf. Abelian function), a generalization of elliptic functions to the case of several complex variables.
are connected by an arbitrary algebraic equation. Along these lines one obtains the Abelian functions (cf. Abelian function), a generalization of elliptic functions to the case of several complex variables.
Elliptic functions and integrals have numerous applications (like special functions) in many branches of analysis, as a means of uniformization in algebraic geometry, and also in mechanics, electrodynamics, and other parts of theoretical physics.
References
| [1] | N.I. Akhiezer, "Elements of the theory of elliptic functions" , Amer. Math. Soc. (1990) (Translated from Russian) |
| [2] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , Springer (1964) pp. Chapt. 3, Abschnitt 2 |
| [3] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) |
| [4] | A.M. Zhuravskii, "Handbook on elliptic functions" , Moscow-Leningrad (1941) (In Russian) |
| [5] | E. Enneper, "Elliptische Funktionen. Theorie und Geschichte" , Halle (1890) |
| [6] | J. Tannéry, J. Molk, "Eléments de la théorie des fonctions elliptiques" , 1–4 , Gauthier-Villars (1893–1902) |
Elliptic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_function&oldid=14556