Difference between revisions of "Elementary flow"
(MSC|60G55|60K25 Category:Stochastic processes) |
(refs format) |
||
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|K}}|| A.Ya. Khinchin, "Mathematical methods in the theory of queueing" , Griffin (1960) (Translated from Russian) | ||
| + | |} | ||
Revision as of 11:10, 12 May 2012
2020 Mathematics Subject Classification: Primary: 60G55 Secondary: 60K25 [MSN][ZBL]
A random sequence of moments of time 
at which the events of a flow of events take place (e.g. a flow of incoming calls at a telephone station), and for which the differences 
satisfy the condition of independence and have the same exponential distribution. An elementary flow with distribution
 | (*) |
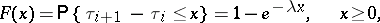is a particular case of a renewal process (cf. Renewal theory). To an elementary flow is related the Poisson process 
equal to the number of events of the flow in the time interval 
. An elementary flow and its related Poisson process satisfy the following conditions.
Stationarity. For any 
, 
the distribution of the random variable
 |
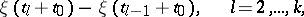does not depend on 
.
Orderliness. The probability of occurrence of two or more events of the flow in the interval 
is equal to 
as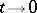 
.
Lack of memory. For 
the random variables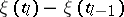 
, 
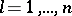, are independent.
It turns out that in these circumstances and under the condition
 |
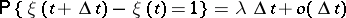the flow is elementary with exponential distribution (*).
References
| [K] | A.Ya. Khinchin, "Mathematical methods in the theory of queueing" , Griffin (1960) (Translated from Russian) |
Elementary flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_flow&oldid=21064