Elementary events
From Encyclopedia of Mathematics
An initial concept in a probability model. In the definition of a probability space 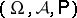 the non-empty set
the non-empty set  is called the space of elementary events and any point
is called the space of elementary events and any point 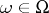 is an elementary event. In an informal approach,
is an elementary event. In an informal approach,  describes the set of all outcomes of a certain random experiment and an elementary event
describes the set of all outcomes of a certain random experiment and an elementary event 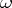 corresponds to an elementary outcome: the experiment ends with one and only one elementary outcome, these outcomes are indecomposable and mutually exclusive. There is a fundamental difference between an elementary event
corresponds to an elementary outcome: the experiment ends with one and only one elementary outcome, these outcomes are indecomposable and mutually exclusive. There is a fundamental difference between an elementary event 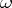 , a point of
, a point of  , and the event
, and the event 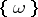 , an element of a certain class of sets
, an element of a certain class of sets 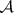 . See Probability theory; Probability space; Random event.
. See Probability theory; Probability space; Random event.
How to Cite This Entry:
Elementary events. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_events&oldid=16149
Elementary events. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_events&oldid=16149
This article was adapted from an original article by A.V. Prokhorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article