Element of best approximation
From Encyclopedia of Mathematics
An element 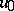 in a given set
in a given set 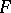 that is a best approximation to a given element
that is a best approximation to a given element  in a metric space
in a metric space 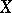 , i.e. is such that
, i.e. is such that
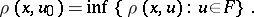 |
This is a generalization of the classical concept of a polynomial of best approximation. The main questions concerning elements of best approximation are: their existence and uniqueness, their characteristic properties (see Chebyshev theorem), the properties of the operator that associates with each element 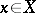 the set of elements of best approximation (see Metric projection; Approximately-compact set), and numerical methods for the construction of elements of best approximation.
the set of elements of best approximation (see Metric projection; Approximately-compact set), and numerical methods for the construction of elements of best approximation.
How to Cite This Entry:
Element of best approximation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Element_of_best_approximation&oldid=18961
Element of best approximation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Element_of_best_approximation&oldid=18961
This article was adapted from an original article by Yu.N. Subbotin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article