Electrodynamics
The branch of physics that studies the mutual interaction of moving rigid or deformable matter and electromagnetic fields. In this vision, electromagnetic fields are created by moving electrically charged matter and, in turn, matter is acted upon by electromagnetic fields. In addition to the Maxwell equations (see also Electromagnetism), the main ingredient therefore is the notion of a ponderomotive force acting on charged particles. Since H.A. Lorentz, this elementary force, called the Lorentz force and acting on a point-like particle of electric charge  , is accepted to be given by
, is accepted to be given by
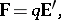 | (a1) |
where  is the electric field in a frame
is the electric field in a frame  co-moving with the charge. The expression of
co-moving with the charge. The expression of  in terms of the electric field
in terms of the electric field  in a fixed laboratory frame
in a fixed laboratory frame  and the velocity
and the velocity  of the particle depend on the relativity theory considered. In the Galilean approximation sufficient for engineering problems, this reads
of the particle depend on the relativity theory considered. In the Galilean approximation sufficient for engineering problems, this reads
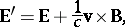 | (a2) |
where 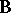 is the magnetic induction in
is the magnetic induction in 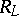 and
and  is the velocity of light in vacuum. The problem of formulating the expressions of the ponderomotive force
is the velocity of light in vacuum. The problem of formulating the expressions of the ponderomotive force  and couple
and couple 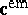 acting on continuous matter in motion and deformation is much more complex and did not receive a unique solution. Sensible expressions may be constructed by performing a volume average in physical space for a representative volume element containing a stable group of point-like electric charges or, better, by performing a statistical average in phase space in a relativistic background. Following along the first line while keeping at most dipoles for electric and magnetic processes, such expressions were computed by G.A. Maugin and A.C. Eringen (1977) in the above "Galilean" approximation as
acting on continuous matter in motion and deformation is much more complex and did not receive a unique solution. Sensible expressions may be constructed by performing a volume average in physical space for a representative volume element containing a stable group of point-like electric charges or, better, by performing a statistical average in phase space in a relativistic background. Following along the first line while keeping at most dipoles for electric and magnetic processes, such expressions were computed by G.A. Maugin and A.C. Eringen (1977) in the above "Galilean" approximation as
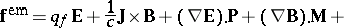 | (a3) |
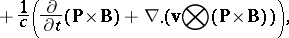 |
and
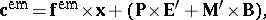 | (a4) |
with which there is associated an energy source per unit volume as
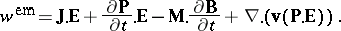 | (a5) |
In these equations, 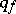 ,
, 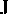 ,
, 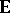 ,
, 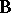 ,
, 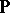 ,
, 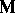 , and
, and  are, respectively, the density of free electric charges per unit volume, the electric current vector, the electric field vector, the magnetic induction vector, the electric polarization vector, and the matter velocity, all expressed in a laboratory frame
are, respectively, the density of free electric charges per unit volume, the electric current vector, the electric field vector, the magnetic induction vector, the electric polarization vector, and the matter velocity, all expressed in a laboratory frame 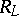 as functions of actual position
as functions of actual position  in physical Euclidean space
in physical Euclidean space 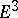 and Newtonian time
and Newtonian time  . A prime denotes a field measured in the co-moving frame. In a vacuum, the three quantities defined by (a3)–(a5) vanish since
. A prime denotes a field measured in the co-moving frame. In a vacuum, the three quantities defined by (a3)–(a5) vanish since 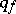 ,
, 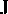 ,
, 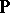 , and
, and 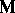 are material fields. In particular, the vanishing of
are material fields. In particular, the vanishing of  yields the following identity (valid only in vacuum):
yields the following identity (valid only in vacuum):
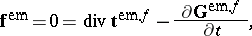 | (a6) |
where
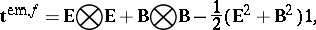 | (a7) |
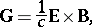 | (a8) |
define the symmetric Maxwell electromagnetic stress tensor  and the electromagnetic momentum
and the electromagnetic momentum 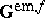 per unit volume in
per unit volume in 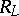 . In a general electrically charged and polarized, magnetized matter, (a6) is replaced by the following identity (Maugin and B. Collet, 1972):
. In a general electrically charged and polarized, magnetized matter, (a6) is replaced by the following identity (Maugin and B. Collet, 1972):
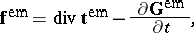 | (a9) |
with the non-symmetric electromagnetic stress tensor  and electromagnetic momentum
and electromagnetic momentum 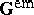 given by the following expressions:
given by the following expressions:
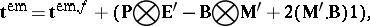 | (a10) |
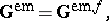 |
while (a5) is transformed to
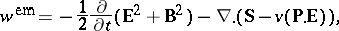 | (a11) |
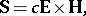 |
where 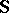 is the Poynting energy flux vector in
is the Poynting energy flux vector in 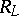 . The divergence of the non-symmetric tensor
. The divergence of the non-symmetric tensor 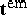 is taken on the first index. However,
is taken on the first index. However,  ,
, 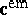 and
and 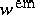 do not relate to a thermodynamically closed system, so that electromagnetic fields are also present as independent variables in the relevant bulk energy density (internal or free energy, depending on the case). This additional dependence allows for a good Galilean-invariant formulation of the electrodynamics of finitely deformable bodies of fluid or solid type. In effect, the electromagneto-mechanical interactions are therefore of two types: through the above-given expressions and through the energy expression. The latter contains such celebrated effects as piezo-electricity (more generally, electro-elasticity), magnetostriction (more generally, magneto-elasticity), as also couplings between the electromagnetic fields and temperature. Coupled thermodynamically irreversible effects include heat and electricity conductions, electrorheology and magnetorheology, electric relaxation coupled to strains, magnetic hysteresis coupled to stresses, etc.
do not relate to a thermodynamically closed system, so that electromagnetic fields are also present as independent variables in the relevant bulk energy density (internal or free energy, depending on the case). This additional dependence allows for a good Galilean-invariant formulation of the electrodynamics of finitely deformable bodies of fluid or solid type. In effect, the electromagneto-mechanical interactions are therefore of two types: through the above-given expressions and through the energy expression. The latter contains such celebrated effects as piezo-electricity (more generally, electro-elasticity), magnetostriction (more generally, magneto-elasticity), as also couplings between the electromagnetic fields and temperature. Coupled thermodynamically irreversible effects include heat and electricity conductions, electrorheology and magnetorheology, electric relaxation coupled to strains, magnetic hysteresis coupled to stresses, etc.
The proper relativistic generalization of 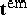 is a recurrent theme of vivid discussions which started with a priori proposals of an electromagnetic energy-momentum tensor by M. Abraham and H. Minkowski early in the 20th century. No definite answer can be given without considering the above-mentioned electromagnetic contributions from the free/internal energy density, i.e. considering the whole "electromagnetic field-plus-matter" thermodynamical system.
is a recurrent theme of vivid discussions which started with a priori proposals of an electromagnetic energy-momentum tensor by M. Abraham and H. Minkowski early in the 20th century. No definite answer can be given without considering the above-mentioned electromagnetic contributions from the free/internal energy density, i.e. considering the whole "electromagnetic field-plus-matter" thermodynamical system.
Among the fields of applications of the classical (non-relativistic) electrodynamics of continuous matter are, in fluids, magnetohydrodynamics, ferrohydrodynamics, electrohydrodynamics, electro- and magnetorheology, and, in solids, electro-elasticity, magneto-elasticity of conductors (perfect conductors are defined by the constraint  ; cf. (a2) for an immediate consequence: the elimination of
; cf. (a2) for an immediate consequence: the elimination of 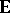 in terms of
in terms of 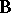 and the matter motion), the magneto-elasticity of ferromagnets, etc. In the relativistic framework, magnetohydrodynamics is relevant to astrophysics and cosmology, while magneto-elasticity may be useful in studying the evolution of solid magnetic starlike objects. All these theories are non-linear to start with and they have been developed in a satisfactory invariant manner during the years 1956–1980, starting with the pioneering work of R.A. Toupin and then extended to the most general cases by A.C. Eringen, H.F. Tiersten, G.A. Maugin and D.F. Nelson. The mathematical properties (e.g., existence of solutions, hyperbolicity of systems, non-linear waves) are generally difficult to study and much remains to be established on solid grounds. Some results by K.O. Friedrichs in relativistic magnetohydrodynamics (1974) and by J. Bazer in magneto-elasticity (1974) are rather exceptional.
and the matter motion), the magneto-elasticity of ferromagnets, etc. In the relativistic framework, magnetohydrodynamics is relevant to astrophysics and cosmology, while magneto-elasticity may be useful in studying the evolution of solid magnetic starlike objects. All these theories are non-linear to start with and they have been developed in a satisfactory invariant manner during the years 1956–1980, starting with the pioneering work of R.A. Toupin and then extended to the most general cases by A.C. Eringen, H.F. Tiersten, G.A. Maugin and D.F. Nelson. The mathematical properties (e.g., existence of solutions, hyperbolicity of systems, non-linear waves) are generally difficult to study and much remains to be established on solid grounds. Some results by K.O. Friedrichs in relativistic magnetohydrodynamics (1974) and by J. Bazer in magneto-elasticity (1974) are rather exceptional.
Quantum electrodynamics (QED), whose formulation is due to F. Dyson, R.P. Feynman, J. Schwinger and S. Tomonaga, is the extension of electrodynamics to the quantum world (electromagnetic moving particles and radiation subjected to quantum-mechanical rules). The main question was to remove the unpleasant divergence of certain quantities, a task fulfilled with success by QED by using sophisticated techniques.
References
| [a1] | J.C. Maxwell, "A treatise on electricity and magnetism" , Clarendon Press (1873) (Reprint of the third (1891) ed.: Dover, 1954) |
| [a2] | L.D. Landau, E.M. Lifshitz, "Electrodynamics of continuous media" , Pergamon (1960) (In Russian) (Revised and enlarged ed.: 1984) |
| [a3] | J.D. Jackson, "Classical electrodynamics" , Wiley (1967) |
| [a4] | S.R. de Groot, L.G. Suttorp, "Foundations of electrodynamics" , North-Holland (1972) |
| [a5] | H.F. Tiersten, "A development of the equations of electromagnetism in material continua" , Tracts in Natural Philosophy , 36 , Springer (1990) |
| [a6] | D.F. Nelson, "Electric, optic and acoustic interactions in dielectrics" , Wiley (1979) |
| [a7] | G.H. Livens, "The theory of electricity" , Cambridge Univ. Press (1962) (Edition: Second) |
| [a8] | G.A. Maugin, "Continuum mechanics of electromagnetic solids" , Applied Math. and Mech. , 33 , North-Holland (1988) |
| [a9] | A.C. Eringen, G.A. Maugin, "Electrodynamics of continua 1–2" , Springer (1990) |
| [a10] | G.A. Maugin, J. Pouget, R. Drouot, B. Collet, "Nonlinear electromechanical couplings" , Wiley (1992) |
| [a11] | M. Ribaric, L. Susteric, "Conservation laws and open questions of classical electrodynamics" , World Sci. (1990) |
| [a12] | A.I. Akhiezer, V.B. Berestetskii, "Quantum electrodynamics" , Wiley (1965) (Edition: Second) |
| [a13] | J. Schwinger, "Particles, sources and fields" , Addison-Wesley (1970) |
| [a14] | A.A. Sokolov, I.M. Temov, V.Ch. Zhukovskii, A.S. Borisov, "Quantum electrodynamics" , Mir (1988) (In Russian) |
Electrodynamics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Electrodynamics&oldid=18872